题目内容
已知O为原点,点A,B的坐标分别为(a,0),(0,a),其中常数a>0.点P在线段AB上,且
=t
(t≥1),则
•
的最大值是( )
| AP |
| AB |
| OA |
| OP |
| A、a2 | B、a |
| C、0 | D、3a |
考点:平面向量数量积的运算
专题:平面向量及应用
分析:由A(a,0),B(0,a),其中常数a>0.点P在线段AB上,且
=t
(t≥1),可得
=
+t
=
(a-ta,ta).得到
•
=-ta2+a2.再利用一次函数的单调性即可得出.
| AP |
| AB |
| OP |
| OA |
| AB |
(a-ta,ta).得到
| OA |
| OP |
解答:
解:∵A(a,0),B(0,a),其中常数a>0.点P在线段AB上,且
=t
(t≥1),
∴
=
+t
=(a,0)+t(-a,a)=(a-ta,ta).
则
•
=(a,0)•(a-ta,ta)=-ta2+a2≤-1×a2+a2=0.
故
•
的最大值是0.
故选:C.
| AP |
| AB |
∴
| OP |
| OA |
| AB |
则
| OA |
| OP |
故
| OA |
| OP |
故选:C.
点评:本题考查了数量积运算、一次函数的单调性,属于基础题.

练习册系列答案
相关题目
两位运动员投篮,投中的概率分别为0.6和0.7,每人各投2次,投中次数相等的概率为( )
| A、0.248 4 |
| B、0.25 |
| C、0.9 |
| D、0.392 4 |
从3名男生和2名女生中选出3名代表去参加辩论比赛,则所选出的3名代表中至少有1名女生的选法共有( )
| A、9种 | B、10种 |
| C、12种 | D、20种 |
已知数列{an}满足a1>0,且an+1=
an,则数列{an}是( )
| 1 |
| 2 |
| A、递增数列 | B、递减数列 |
| C、常数列 | D、摆动数列 |
在△ABC中,c=3,A=30°,B=120°,则△ABC的面积为( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
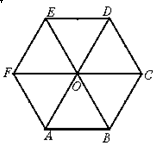 如图,设O是正六边形ABCDEF的中心,在向量
如图,设O是正六边形ABCDEF的中心,在向量| OB |
| OC |
| OD |
| OE |
| OF |
| AB |
| BC |
| CD |
| EF |
| DE |
| FA |
| OA |
| A、1个 | B、2个 | C、3个 | D、4个 |
从点P(1,-2)引圆(x+1)2+(y-1)2=4的切线,则切线长是( )
| A、4 | B、3 | C、2 | D、1 |
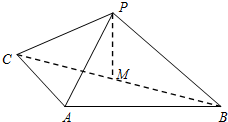 如图,△PAB是边长为2的正三角形,平面PAB外一动点C满足下面条件:PC=PA,AC⊥AB.
如图,△PAB是边长为2的正三角形,平面PAB外一动点C满足下面条件:PC=PA,AC⊥AB.