题目内容
设a＞0，b＞1，若a+b=2，则
+
-1的最小值为 ．
| 2 |
| a |
| 1 |
| b |
考点：基本不等式
专题：不等式的解法及应用
分析：原式转化为
+
-1=
+
-1=
+
+
，再利用基本不等式即可求出最小值
| 2 |
| a |
| 1 |
| b |
| a+b |
| a |
| a+b |
| 2b |
| b |
| a |
| a |
| 2b |
| 1 |
| 2 |
解答：
解：∵a+b=2，a＞0，b＞1，
∴
+
-1=
+
-1=1+
+
+
-1=
+
+
≥2
+
=
+
，当且仅当a=4-2
，b=2
-2取等号，
∴
+
-1的最小值为
+
，
故答案为：
+
，
∴
| 2 |
| a |
| 1 |
| b |
| a+b |
| a |
| a+b |
| 2b |
| b |
| a |
| a |
| 2b |
| 1 |
| 2 |
| b |
| a |
| a |
| 2b |
| 1 |
| 2 |
|
| 1 |
| 2 |
| 2 |
| 1 |
| 2 |
| 2 |
| 2 |
∴
| 2 |
| a |
| 1 |
| b |
| 2 |
| 1 |
| 2 |
故答案为：
| 2 |
| 1 |
| 2 |
点评：本题主要考查基本不等式的性质的应用，关键是注意取得等号的条件，属于基础题
练习册系列答案
通城学典默写能手系列答案
相关题目
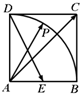如图在边长为2的正方形ABCD中，E为边AB的中点，P为以A为圆心、AB为半径的圆弧上的任意一点，设向量
如图甲所示，点E为矩形ABCD边CD的中点，AB=2，AD=