题目内容
如图，在正方体ABCD-A1B1C1D1中，E，F分别为棱AD，AB的中点．
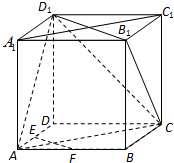
（Ⅰ）求证：EF∥平面CB1D1；
（Ⅱ）求异面直线EF与CD1所成角．
（Ⅰ）求证：EF∥平面CB1D1；
（Ⅱ）求异面直线EF与CD1所成角．
考点：异面直线及其所成的角,直线与平面平行的判定
专题：空间角
分析：（Ⅰ）连结BD，则EF∥BD，从而四边形是BB1D1D是平行四边形，由此能证明EF∥平面CB1D1．
（Ⅱ）连接A1B，A1D，则四边形BCD1A1是平行四边形，EF∥BD，从而∠A1BD就是异面直线EF与CD1所成角，由此能求出异面直线EF与CD1所成角．
（Ⅱ）连接A1B，A1D，则四边形BCD1A1是平行四边形，EF∥BD，从而∠A1BD就是异面直线EF与CD1所成角，由此能求出异面直线EF与CD1所成角．
解答：
（Ⅰ）证明：连结BD，∵E，F分别是AD，AB的中点，∴EF∥BD，
∵BB1∥DD1，BB1=DD1，
∴四边形是BB1D1D是平行四边形，
∴BD∥B1D1，∴EF∥BD，
∵B1D1?平面B1D1C，EF?面B1D1C，
∴EF∥平面CB1D1．
（Ⅱ）解：连接A1B，A1D，∵AD
BC，AD
A1D1，
∴BC
A1D1，∴四边形BCD1A1是平行四边形，…（8分）
∴BA1∥CD1，又∵EF∥BD，
∴∠A1BD就是异面直线EF与CD1所成角 …（10分）
∵在正方体AC1中A1B=A1D=BD，
∴∠A1BD=60°，
∴异面直线EF与CD1所成角为60°．…（12分）
∵BB1∥DD1，BB1=DD1，
∴四边形是BB1D1D是平行四边形，
∴BD∥B1D1，∴EF∥BD，
∵B1D1?平面B1D1C，EF?面B1D1C，
∴EF∥平面CB1D1．
（Ⅱ）解：连接A1B，A1D，∵AD
| ||
. |
| ||
. |
∴BC
| ||
. |
∴BA1∥CD1，又∵EF∥BD，
∴∠A1BD就是异面直线EF与CD1所成角 …（10分）
∵在正方体AC1中A1B=A1D=BD，
∴∠A1BD=60°，
∴异面直线EF与CD1所成角为60°．…（12分）
点评：本题考查直线与平面平行的证明，考查异面直线所成角的求法，是中档题，解题时要注意线线、线面、面面间的位置关系和性质的合理运用．
练习册系列答案
提分百分百检测卷系列答案
宝贝计划期末冲刺夺100分系列答案
相关题目
函数f（x）=cos2x-2
sinxcosx下列命题中正确的是（ ）
（1）若存在x1，x2有x1-x2=z时，f（x1）=f（x2）成立
（2）f（x）在[-
，
]是单调递增
（3）函数f（x）关于点（
，0）成中心对称图象
（4）将函数f（x）的图象向左平移
个单位后将与y=2sin2x重合．
| 3 |
（1）若存在x1，x2有x1-x2=z时，f（x1）=f（x2）成立
（2）f（x）在[-
| π |
| 6 |
| π |
| 3 |
（3）函数f（x）关于点（
| π |
| 12 |
（4）将函数f（x）的图象向左平移
| 5π |
| 12 |
| A、（1）（2） |
| B、（ 1）（3） |
| C、（ 1）（2）（3） |
| D、（1）（3）（4） |
在正方体ABCD-A1B1C1D1中，P，Q分别是AB，B1C1上的点AP=B1Q，N是PQ的中点，M是正方形ABB1A1的中心．求证：在正方体ABCD-A1B1C1D1中，M是棱DD1的中点，点O为底面ABCD的中心，P为棱A1B1上任一点，则异面直线OP与AM所成的角的大小为（ ）
| A、30° | B、60° |
| C、90° | D、120° |
