题目内容
已知点（3，1）和（4，-6）在直线2x-y+a=0的两侧，则a的取值范围为 ．
考点：二元一次不等式（组）与平面区域
专题：计算题
分析：由已知点（3，1）和（4，-6）在直线2x-y+a=0的两侧，我们将两点坐标代入直线方程所得符号相反，则我们可以构造一个关于a的不等式，解不等式即可得到答案．
解答：
解：若点（3，1）和（4，-6）在直线2x-y+a=0的两侧，
则[3×2-1+a]×[3×（2）+6+a]＜0
即（a+14）（a+5）＜0
解得-14＜a＜-5，
故答案为：-14＜a＜-5．
则[3×2-1+a]×[3×（2）+6+a]＜0
即（a+14）（a+5）＜0
解得-14＜a＜-5，
故答案为：-14＜a＜-5．
点评：本题考查的知识点是二元一次不等式与平面区域，根据两点在直线两侧，则两点的坐标代入直线方程所得符号相反构造不等式是解答本题的关键．
练习册系列答案
名校通行证有效作业系列答案
相关题目
已知直线z的极坐标方程为ρcos(θ-
) =
，点A的极坐标为（4，
），则点A到直线l的距离为（ ）
| 3π |
| 4 |
| 2 |
| π |
| 4 |
A、
| ||||
| B、1 | ||||
C、
| ||||
| D、2 |
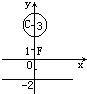如图，已知F（0，1），直线l：y=-2，圆C：x2+（y-3）2=1