题目内容
设函数f(x)=lnx+ex,g(x)=ex+
x2-ax(a∈R)(e=2.71828…是自然对数的底数)
(1)当a=
,设F(x)=f(x)-g(x),求F(x)的单调区间;
(2)定义:若函数φ(x)在定义域为[m,n](m<n)上的值域为[m,n],则称区间[m,n]为函数φ(x)的“同域区间”,在(1)的条件下,证明:函数F(x)在区间(0,2)内存在“同域区间”;
(3)当a>1时,对于区间(2,3)内任意两个不相等的实数x1,x2都有|f(x1)-f(x2)|>|g(x1)-g(x2)|成立,求a的取值范围.
| 1 |
| 2 |
(1)当a=
| 3 |
| 2 |
(2)定义:若函数φ(x)在定义域为[m,n](m<n)上的值域为[m,n],则称区间[m,n]为函数φ(x)的“同域区间”,在(1)的条件下,证明:函数F(x)在区间(0,2)内存在“同域区间”;
(3)当a>1时,对于区间(2,3)内任意两个不相等的实数x1,x2都有|f(x1)-f(x2)|>|g(x1)-g(x2)|成立,求a的取值范围.
考点:利用导数研究函数的单调性,利用导数求闭区间上函数的最值
专题:导数的综合应用
分析:(1)求出F(x)=f(x)-g(x)的表达式,求函数的导数即可求F(x)的单调区间,
(2)根据“同域区间”的定义,建立方程关系,即可得到结论.
(3)根据不等式恒成立问题,进行转化,即可得到结论.
(2)根据“同域区间”的定义,建立方程关系,即可得到结论.
(3)根据不等式恒成立问题,进行转化,即可得到结论.
解答:
解:(1)当a=
,设F(x)=f(x)-g(x)=lnx-
x2+
x,
则F(x)的定义域为(0,+∞),
则F′(x)=
-x+
=-
,
由F′(x)>0,解得0<x<2,此时函数单调递增.
F′(x)<0,解得x>2,此时函数单调递减.
(2)设F(x)=lnx-
x2+
x的定义域为[m,n],假设存在“同域区间”,
则由(1)知,F(x)在区间(0,2)上单调递增,
即
,则
,
也就是方程lnx-
x2+
=x在区间(0,2)上存在两个相异的实根,
即2lnx-x2+x=0在区间(0,2)上存在两个相异的实根,
即T(x)=2lnx-x2+x,则T′(x)=
-2x+1单调递减,
当x∈(0,2)时,T′(x)=
-2x+1<0,
设m(x)=T′(x)=
-2x+1,
则m(
)=2e+1-
>0,m(2)=-2<0,即在区间(
,2)上必存在唯一的点x0∈(
,2)使m(x0)=0,
当x∈(
,x0),m(x)>0,此时函数m(x)单调递增,
当x∈(x0,2),m(x)<0,此时函数m(x)单调递减,
T(
)=
<0,
∵m(1)=1>0,∴x0>1,即T(x)在(1,x0)上递增,
T(x0)>T(1)=0,T(2)=2ln2-4+2=2ln2-2=2(ln2-1)<0,
∴T(x)=2lnx-x2+x,在区间(
,2)上有两个不相等的解,
即方程2lnx-x2+x=0在区间(
,2)上有两个不相等的实根,
从而函数F(x)在区间(0,2)内存在“同域区间”;
(3)不妨设2<x1<x2<3,则f(x)=lnx+ex,在区间(2,3)上单调递增,
则有|f(x1)-f(x2)|=f(x2)-f(x1),
∴|f(x1)-f(x2)|>|g(x1)-g(x2)|等价为|g(x1)-g(x2)|<f(x2)-f(x1),
则f(x1)-f(x2)<|g(x1)-g(x2)|<f(x2)-f(x1),
即f(x1)-g(x1)<f(x2)-g(x2)且g(x1)+f(x1)<g(x2)+f(x2)恒成立,
从而f(x)-g(x)在(2,3)上单调递增,求f(x)+g(x)在(2,3)上单调递增,
即[f(x)-g(x)]′>0,[f(x)+g(x)]′>0,
∴命题等价为当x∈(2,3)下
恒成立,
即
,解得
≤a≤
+2e2.
| 3 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
则F(x)的定义域为(0,+∞),
则F′(x)=
| 1 |
| x |
| 3 |
| 2 |
| (2x+1)(x-2) |
| 2x |
由F′(x)>0,解得0<x<2,此时函数单调递增.
F′(x)<0,解得x>2,此时函数单调递减.
(2)设F(x)=lnx-
| 1 |
| 2 |
| 3 |
| 2 |
则由(1)知,F(x)在区间(0,2)上单调递增,
即
|
|
也就是方程lnx-
| 1 |
| 2 |
| 3 |
| 2 |
即2lnx-x2+x=0在区间(0,2)上存在两个相异的实根,
即T(x)=2lnx-x2+x,则T′(x)=
| 2 |
| x |
当x∈(0,2)时,T′(x)=
| 2 |
| x |
设m(x)=T′(x)=
| 2 |
| x |
则m(
| 1 |
| e |
| 2 |
| e |
| 1 |
| e |
| 1 |
| e |
当x∈(
| 1 |
| e |
当x∈(x0,2),m(x)<0,此时函数m(x)单调递减,
T(
| 1 |
| e |
| e(-2e+1)-1 |
| e2 |
∵m(1)=1>0,∴x0>1,即T(x)在(1,x0)上递增,
T(x0)>T(1)=0,T(2)=2ln2-4+2=2ln2-2=2(ln2-1)<0,
∴T(x)=2lnx-x2+x,在区间(
| 1 |
| e |
即方程2lnx-x2+x=0在区间(
| 1 |
| e |
从而函数F(x)在区间(0,2)内存在“同域区间”;
(3)不妨设2<x1<x2<3,则f(x)=lnx+ex,在区间(2,3)上单调递增,
则有|f(x1)-f(x2)|=f(x2)-f(x1),
∴|f(x1)-f(x2)|>|g(x1)-g(x2)|等价为|g(x1)-g(x2)|<f(x2)-f(x1),
则f(x1)-f(x2)<|g(x1)-g(x2)|<f(x2)-f(x1),
即f(x1)-g(x1)<f(x2)-g(x2)且g(x1)+f(x1)<g(x2)+f(x2)恒成立,
从而f(x)-g(x)在(2,3)上单调递增,求f(x)+g(x)在(2,3)上单调递增,
即[f(x)-g(x)]′>0,[f(x)+g(x)]′>0,
∴命题等价为当x∈(2,3)下
|
即
|
| 8 |
| 3 |
| 5 |
| 2 |
点评:本题主要考查函数的性质和导数之间的关系,综合性较强,运算量较大,难度非常大.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
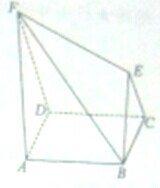 在如图所示的几何体中,四边形ABCD为正方形,DF∥CE,DF⊥DC,且DF=2AD=2CE,AF=
在如图所示的几何体中,四边形ABCD为正方形,DF∥CE,DF⊥DC,且DF=2AD=2CE,AF=