已知双曲线的左.右焦点分别为F1.F2.且双曲线上存在异于顶点的一点P.满足tan∠PF1F22=3tan∠PF2F12.则该双曲线离心率为( ) A.2B.3C.3D.5 题目和参考答案——青夏教育精英家教网—

题目内容

已知双曲线的左、右焦点分别为F₁、F₂，且双曲线上存在异于顶点的一点P，满足tan

∠PF1F2

=3tan

∠PF2F1

，则该双曲线离心率为（　　）

A、2

B、3

C、

D、

考点：双曲线的简单性质

专题：计算题,圆锥曲线的定义、性质与方程

分析：设△PF₁F₂的内切圆的圆心为O₁，半径为r，F₁C=x，则F₂C=3x，可得F₁F₂=4x=2c，PF₂-PF₁=F₂B-F₁A=F₂C-F₁C=2x=2a，即可求出双曲线离心率．

解答：

解：设△PF₁F₂的内切圆的圆心为O₁，半径为r，F₁C=x，则F₂C=3x，
∴F₁F₂=4x=2c，
∵PF₂-PF₁=F₂B-F₁A=F₂C-F₁C=2x=2a，
∴e=

=2．
故选：A．

点评：本题主要考查了双曲线的简单性质，考查了双曲线的定义的灵活运用，属于中档题．

练习册系列答案

同步练习册外语教学与研究出版社系列答案

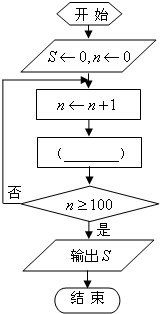
A、S←2^-1+2^-2+…+2^-n

B、S←S+2^-n

C、S←2^-1+2^-2+…+2^-100

D、S←S+2^-n-1

函数y=f（x）是定义在R上的可导函数，则x=x₀为函数y=f（x）的极值点是f′（x₀）=0的（　　）

对任意复数z=x+yi（x，y∈R），i为虚数单位，则下列结论正确的是（　　）

三菱柱的侧棱与底面垂直，且底面是边长为2的等边三角形，其正视图（如图）的面积为8，则该三棱柱的体积为（　　）

正项等比数列{a_n}中，如果a₁+a₄+a₇=3，a₃+a₆+a₉=27，则数列{a_n}前9项的和为（　　）

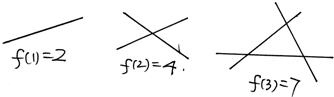对于问题：“两两相交且任三条不共点的n条直线把平面分为f（n）部分”，我们由归纳推理得到f（10）=（　　）

=1（a＞0，b＞0），右焦点F到渐近线的距离小于等于a，则该双曲线离心率的取值范围为（　　）

设函数f（x）=lnx+e^x，g（x）=e^x+

x²-ax（a∈R）（e=2.71828…是自然对数的底数）
（1）当a=

，设F（x）=f（x）-g（x），求F（x）的单调区间；
（2）定义：若函数φ（x）在定义域为[m，n]（m＜n）上的值域为[m，n]，则称区间[m，n]为函数φ（x）的“同域区间”，在（1）的条件下，证明：函数F（x）在区间（0，2）内存在“同域区间”；
（3）当a＞1时，对于区间（2，3）内任意两个不相等的实数x₁，x₂都有|f（x₁）-f（x₂）|＞|g（x₁）-g（x₂）|成立，求a的取值范围．

试题分类