题目内容
设函数f(x)=
x3-
ax2+(a-1)x,
(1)当a=1时,求曲线y=f(x)在点(0,0)处的切线方程;
(2)当a为何值时,函数y=f(x)有极值?并求出极大值.
| 1 |
| 3 |
| 1 |
| 2 |
(1)当a=1时,求曲线y=f(x)在点(0,0)处的切线方程;
(2)当a为何值时,函数y=f(x)有极值?并求出极大值.
考点:利用导数研究函数的极值,利用导数研究曲线上某点切线方程
专题:导数的综合应用
分析:(1)当a=1时,k=f′(0)=0,则曲线y=f(x)在点(0,0)处的切线方程y=0;
(2)显然,当a-1≠1时,即 a≠2时函数有极值,通过讨论①当a<2时,即a-1<1时②当a>2时,即a-1>1时的函数的单调性,从而找到函数的极大值.
(2)显然,当a-1≠1时,即 a≠2时函数有极值,通过讨论①当a<2时,即a-1<1时②当a>2时,即a-1>1时的函数的单调性,从而找到函数的极大值.
解答:
解:f′(x)=x2-ax+a-1=(x-1)[x-(a-1)]
(1)当a=1时,k=f′(0)=0,则曲线y=f(x)在点(0,0)处的切线方程y=0;
(2)显然,当a-1≠1时,即 a≠2时函数有极值.
①当a<2时,即a-1<1时,有
此时,函数函数y=f(x)极大值为f(a-1)=
(a-1)2.
②当a>2时,即a-1>1时,有
此时,函数y=f(x)极大值为f(1)=
-
.
综上,函数y=f(x)极大值为f(x)极大值=
.
(1)当a=1时,k=f′(0)=0,则曲线y=f(x)在点(0,0)处的切线方程y=0;
(2)显然,当a-1≠1时,即 a≠2时函数有极值.
①当a<2时,即a-1<1时,有
| x | (-∞,a-1) | a-1 | (a-1,1) | 1 | (1,+∞) |
| f′(x) | + | 0 | - | 0 | + |
| f(x) | 递增 | 递减 | 递增 |
| 4-a |
| 6 |
②当a>2时,即a-1>1时,有
| x | (-∞,1) | 1 | (1,a-1) | a-1 | (a-1,+∞) |
| f′(x) | + | 0 | - | 0 | + |
| f(x) | 递增 | 递减 | 递增 |
| a |
| 2 |
| 2 |
| 3 |
综上,函数y=f(x)极大值为f(x)极大值=
|
点评:本题考察了函数的单调性,函数的极值问题,导数的应用,渗透了分类讨论思想,是一道基础题.

练习册系列答案
 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案
相关题目
交通局对上班、下班高峰时的车速情况作抽样调查,行驶时速(单位:km/h)的统计数据用茎叶图表示如图:
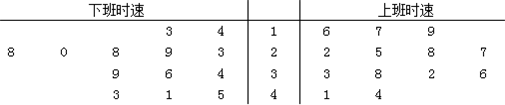
设上、下班时速的平均数分别为
上、
下,中位数分别为
上、
下,则( )

设上、下班时速的平均数分别为
. |
| x |
. |
| x |
. |
| m |
. |
| m |
A、
| ||||||||
B、
| ||||||||
C、
| ||||||||
D、
|
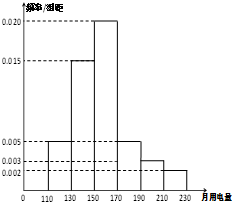 2013年第三季度,国家电网决定对城镇居民民用电计费标准做出调整,并根据用电情况将居民分为三类:第一类的用电区间在(0,170],第二类在(170,260],第三类在(260,+∞)(单位:千瓦时).某小区共有1000户居民,现对他们的用电情况进行调查,得到频率分布直方图如图所示.
2013年第三季度,国家电网决定对城镇居民民用电计费标准做出调整,并根据用电情况将居民分为三类:第一类的用电区间在(0,170],第二类在(170,260],第三类在(260,+∞)(单位:千瓦时).某小区共有1000户居民,现对他们的用电情况进行调查,得到频率分布直方图如图所示. 如图所示,四棱锥P-ABCD的底面ABCD是矩形,侧面PAD是等腰直角三角形,
如图所示,四棱锥P-ABCD的底面ABCD是矩形,侧面PAD是等腰直角三角形,