题目内容
函数f(x)=lnx-x+2的零点所在的区间为( )
| A、(4,5) |
| B、(1,2) |
| C、(2,3) |
| D、(3,4) |
考点:利用导数研究函数的极值
专题:函数的性质及应用
分析:可逐个求出f(1),f(2),f(3),f(4),f(5)的值,从而得出结论.
解答:
解:∵f(1)=ln1+1>0,f(2)=ln2>0,f(3)=ln3-1>0,
f(4)=ln4-2<0,f(5)=ln5-3<0,
∴函数f(x)=lnx-x+2的零点所在的区间为(3,4);
故选:D.
f(4)=ln4-2<0,f(5)=ln5-3<0,
∴函数f(x)=lnx-x+2的零点所在的区间为(3,4);
故选:D.
点评:本题考察了函数的零点问题,可采用特殊值法逐个代入,本题是一道基础题.

练习册系列答案
相关题目
已知双曲线C:
-
=1(a>0,b>0)的离心率为
,则C的渐近线方程为( )
| x2 |
| a2 |
| y2 |
| b2 |
| 5 |
| A、y=±2x | ||
B、y=±
| ||
C、y=±
| ||
D、y=±
|
以原点为中心,焦点在y轴上的双曲线C的一个焦点为F(0,2
),一个顶点为A(0,-2),则双曲线C的方程为( )
| 2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
交通局对上班、下班高峰时的车速情况作抽样调查,行驶时速(单位:km/h)的统计数据用茎叶图表示如图:
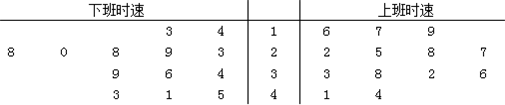
设上、下班时速的平均数分别为
上、
下,中位数分别为
上、
下,则( )

设上、下班时速的平均数分别为
. |
| x |
. |
| x |
. |
| m |
. |
| m |
A、
| ||||||||
B、
| ||||||||
C、
| ||||||||
D、
|
在区间[1,3]上任取一数,则这个数大于等于1.5的概率为( )
| A、0.25 | B、0.5 |
| C、0.6 | D、0.75 |
参数方程
(t为参数)表示什么曲线( )
|
| A、一条直线 | B、一个半圆 |
| C、一条射线 | D、一个圆 |
化简
-
+
=( )
| AC |
| DC |
| DA |
A、
| ||
B、
| ||
C、
| ||
D、
|