题目内容

13．已知sin2θ-2cosθ=-2，那么cos2θ-2sinθ=（　　）
A．1B．-2C．-1D．2

分析 由条件利用同角三角函数的基本关系求得cosθ=1，sinθ=0，从而求得cos2θ-2sinθ的值．

解答 解：∵sin2θ-2cosθ=-2，∴cos2θ+2cosθ=3，∴cosθ=1，sinθ=0，
那么cos2θ-2sinθ=1-0=1，
故选：A．

点评 本题主要考查同角三角函数的基本关系，属于基础题．

练习册系列答案
相关题目
3．直线x=3与直线2x+y-1=0的夹角是$\frac{π}{2}$-arctan2．
4．求y=ax•sinx的导数．
1．若$\root{4}{4{a}^{2}-4a+1}$=$\root{3}{1-2a}$，则实数a的取值范围是（　　）
A．a=$\frac{1}{2}$B．a=$\frac{1}{2}$或a=0C．a=0D．a≤$\frac{1}{2}$
8．函数y=$\frac{{x}^{2}-8}{\sqrt{{x}^{2}-9}}$的最小值是2．
18．已知命题p：x2+2x-2＞0，命题q：x＞m，且￢q的一个充分不必要条件是￢p，则实数m的取值范围是[-1+$\sqrt{3}$，+∞）．
5．在等比数列{an}中．
（1）a3=3，q=-2，则a10=-384；
（2）q=2，则$\frac{2{a}_{1}+{a}_{2}}{2{a}_{3}+{a}_{4}}$=$\frac{1}{4}$；
（3）a3+a6=36，a4+a7=18，an=$\frac{1}{2}$，则n=9．
2．若cos（-820°）=t，则tan（-440°）=（　　）
A．-$\frac{\sqrt{1-{t}^{2}}}{t}$B．$\frac{\sqrt{1-{t}^{2}}}{t}$C．$\frac{\sqrt{1+{t}^{2}}}{t}$D．-$\frac{\sqrt{1+{t}^{2}}}{t}$
13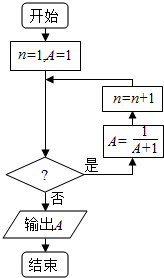．已知数列{an}中，${a_1}=1，{a_{n+1}}=\frac{1}{{1+{a_n}}}$，若利用下面程序框图计算该数列的第2016项，则判断框内的条件是（　　）
A．n≤2014B．n≤2016C．n≤2015D．n≤2017

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网