题目内容
某同学参加科普知识竞赛，需回答三个问题，竞赛规则规定；每题回答正确得100分，回答不正确得-100分，假设这名同学每题回答正确的概率均为0.8，且各题回答正确与否相互之间没有影响
求这名同学回答这三个问题的总得分X的概率分布和均值．
求这名同学回答这三个问题的总得分X的概率分布和均值．
考点：离散型随机变量的期望与方差,离散型随机变量及其分布列
专题：概率与统计
分析：由已知得这名学生回答正确的问题的个数Y～B（3，
），这名同学回答这三个问题的总得分X的可能取值为-300，-100，100，300，由此能求出这名同学回答这三个问题的总得分X的概率分布和均值．．
| 4 |
| 5 |
解答：
解：由已知得这名学生回答正确的问题的个数Y～B（3，
），
这名同学回答这三个问题的总得分X的可能取值为-300，-100，100，300，
P（X=-300）=P（Y=0）=
(
)3=
，
P（X=-100）=P（Y=1）=
(
)(
)2=
，
P（X=100）=P（Y=2）=
(
)2(
)=
，
P（X=300）=P（Y=3）=(
)3=
，
∴X的分布列为：
EX=-300×
+(-100)×
+100×
+300×
=180．
| 4 |
| 5 |
这名同学回答这三个问题的总得分X的可能取值为-300，-100，100，300，
P（X=-300）=P（Y=0）=
| C | 0 3 |
| 1 |
| 5 |
| 1 |
| 125 |
P（X=-100）=P（Y=1）=
| C | 1 3 |
| 4 |
| 5 |
| 1 |
| 5 |
| 12 |
| 125 |
P（X=100）=P（Y=2）=
| C | 2 3 |
| 4 |
| 5 |
| 1 |
| 5 |
| 48 |
| 125 |
P（X=300）=P（Y=3）=(
| 4 |
| 5 |
| 64 |
| 125 |
∴X的分布列为：
| X | -300 | -100 | 100 | 300 | ||||||||
| P |
|
|
|
|
| 1 |
| 125 |
| 12 |
| 125 |
| 48 |
| 125 |
| 64 |
| 125 |
点评：本题考查离散型随机变量的分布列和数学期望的求法，是中档题，解题时要认真审题，在历年高考中都是必考题型之一．
练习册系列答案
亮点激活精编提优100分大试卷系列答案
相关题目
下列命题的说法错误的是（ ）
| A、命题“若x2-4x-3=0，则x=1”的逆否命题为“若x≠1，则x2-4x-3≠0” | ||||
| B、已知a，b，c是△A BC的三条边，△A BC是等边三角形的充要条件是a2+b2+c2=ab+ac+bc | ||||
C、命题“若α=
| ||||
| D、若命题p：b=0，命题q：函数f（x）=ax2+bx+c是偶函数，则p是q的充分不必要条件 |
如图是函数y=f（x）的导函数的图象，则正确的判断是（ ）
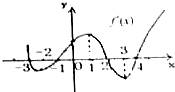
| A、f（x）在（-2，1）上是增函数 |
| B、x=1是f（x）的极大值点 |
| C、f（x）在（-1，2）上是增函数，在（2，4）上是减函数 |
| D、x=3是f（x）的极小值点 |
