题目内容
18．已知2sinx=1+cosx，则$cot\frac{x}{2}$=（ ）| A． | 2 | B． | 2或$\frac{1}{2}$ | C． | 2或0 | D． | $\frac{1}{2}$或0 |
分析 推导出cot$\frac{x}{2}$=$\frac{cos\frac{x}{2}}{sin\frac{x}{2}}$=$\frac{1+cosx}{sinx}$，由此能求出结果．
解答 解：∵2sinx=1+cosx，
∴cot$\frac{x}{2}$=$\frac{cos\frac{x}{2}}{sin\frac{x}{2}}$=$\frac{2co{s}^{2}\frac{x}{2}}{2sin\frac{x}{2}cos\frac{x}{2}}$=$\frac{1+cosx}{sinx}$，
2sinx=1+cosx，
∴当cosx=-1时，sinx=0，无解；
当cosx≠-1时，cot$\frac{x}{2}$=$\frac{1+cosx}{sinx}$=2．
当cosx=-1时，无解．
故选：A．
点评 本题考查三角函数的化简求值，考查同角三角函数关系式、二倍角公式、降幂公式，考查推理论证能力、运算求解能力，考查转化化归思想，是中档题．
练习册系列答案
浙江名校名师金卷系列答案
全优冲刺100分系列答案
相关题目
8．设数列{an}为等差数列，Sn为其前n项和，若S1≤13，S4≥10，S5≤15，则a4的最大值为（ ）
| A． | 3 | B． | 4 | C． | -7 | D． | -5 |
9．命题“?n∈N，f（n）∉N且f（n）≤n”的否定形式是（ ）
| A． | ?n∈N，f（n）∈N且f（n）＞n | B． | ?n0∈N，f（n0）∈N且f（n0）＞n0 | ||
| C． | ?n∈N，f（n）∈N或f（n）＞n | D． | ?n0∈N，f（n0）∈N或f（n0）＞n0 |
3．已知集合A={0，1，2，3，4}，B={x|x=2n+1，n∈A}，则A∩B等于（ ）
| A． | {1，3，5} | B． | {3} | C． | {5，7，9} | D． | {1，3} |
10．
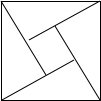在如图所示的“勾股圆方图”中，四个相同的直角三角形与中间的小正方形拼成一个边长为2的大正方形，若直角三角形中较小的锐角α=$\frac{π}{6}$，现在向该大正方形区域内随机地投掷一枚飞镖，则飞镖落在小正方形内的概率是（ ）
在如图所示的“勾股圆方图”中，四个相同的直角三角形与中间的小正方形拼成一个边长为2的大正方形，若直角三角形中较小的锐角α=$\frac{π}{6}$，现在向该大正方形区域内随机地投掷一枚飞镖，则飞镖落在小正方形内的概率是（ ）| A． | 1-$\frac{\sqrt{3}}{2}$ | B． | $\frac{\sqrt{3}}{2}$ | C． | $\frac{4-\sqrt{3}}{4}$ | D． | $\frac{\sqrt{3}}{4}$ |