题目内容
14.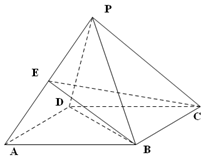 如图,四棱锥P-ABCD的底面ABCD是边长为2的菱形,∠BAD=60°,PB=PD=2,PA=$\sqrt{6}$,E为PA的中点,
如图,四棱锥P-ABCD的底面ABCD是边长为2的菱形,∠BAD=60°,PB=PD=2,PA=$\sqrt{6}$,E为PA的中点,(1)证明:PC∥面EBD;
(2)求三棱锥P-BCE的体积.
分析 (1)如图所示,连接AC交BD于点O.由底面ABCD是菱形,可得OA=OC,利用三角形的中位线定理可得OE∥PC,再利用线面平行的判定定理即可证明PC∥平面EBD.
(2)由于点E是PA的中点,可得V三棱锥P-BCE=$\frac{1}{2}$V三棱锥A-PBC.由O点是AC的中点,可得V三棱锥A-PBC=2V三棱锥A-POB=$\frac{1}{3}×\frac{1}{2}×$OP×OB×OA,即可得出.
解答 (1)证明:如图所示,连接AC交BD于点O.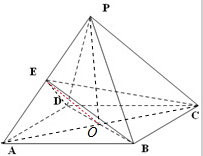
∵底面ABCD是菱形,
∴OA=OC,
又∵E为PA的中点,∴EO∥PC,
而PC?平面BED,EO?平面BED,
∴PC∥平面EBD.
(2)∵点E是PA的中点,∴V三棱锥P-BCE═$\frac{1}{2}$V三棱锥A-PBC.由O点是AC的中点,
可得V三棱锥A-PBC=2V三棱锥A-POB=$\frac{1}{3}×\frac{1}{2}×$OP×OB×OA=$\frac{1}{3}×\sqrt{3}×1×\sqrt{3}=1$.
∴得V三棱锥P-BCE=$\frac{1}{2}$V三棱锥A-PBC=$\frac{1}{2}$
点评 题考查了菱形的性质、三角形的中位线定理、线面平行的判定定理、三棱锥的体积计算公式,考查了了推理能力与计算能力,属于中档题

练习册系列答案
 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案
相关题目
2.张家的3个鸡仔钻进了李家装有3个鸡仔的鸡笼里,现打开笼门,让鸡仔一个一个地走出来,若第一个走出来的是张家的鸡仔,那么第二个走出的也是张家的鸡仔的概率是( )
| A. | $\frac{2}{5}$ | B. | $\frac{2}{3}$ | C. | $\frac{1}{5}$ | D. | $\frac{3}{5}$ |
9.设z=-1+3i,则z的共轭复数为( )
| A. | -1+3i | B. | -1-3i | C. | 1+3i | D. | 1-3i |
19.复数z=a+i(a∈R)的虚部为( )
| A. | 1 | B. | i | C. | -1 | D. | -i |
3.如图所示的程序框图,运行后输出的结果为( )


| A. | 4 | B. | 8 | C. | 16 | D. | 32 |