题目内容
已知函数f(x)=-x2-2x,g(x)=
,若方程g[f(x)]-a=0的实数根的个数有3个,则实数a的值是 .
|
考点:函数解析式的求解及常用方法
专题:函数的性质及应用
分析:分别作出两个函数的图象,根据两个图象之间的关系即可得到结论.
解答:
解: ∵当x>0时,g(x)=x+
∵当x>0时,g(x)=x+
≥2
=2×
=1,当且仅当x=
,即x=
时取等号.
当x≤0时,g(x)=x+1≤1,
而f(x)=-x2-2x=-(x+1)2+1≤1,
设t=f(x),
则方程g[f(x)]-a=0等价为g(t)=a,
要使方程g[f(x)]-a=0的实数根的个数有3个,
则t=1且t<1,当t=1时,g(1)=1+
=
=a.
故答案为:
 ∵当x>0时,g(x)=x+
∵当x>0时,g(x)=x+| 1 |
| 4x |
x•
|
| 1 |
| 2 |
| 1 |
| 4x |
| 1 |
| 2 |
当x≤0时,g(x)=x+1≤1,
而f(x)=-x2-2x=-(x+1)2+1≤1,
设t=f(x),
则方程g[f(x)]-a=0等价为g(t)=a,
要使方程g[f(x)]-a=0的实数根的个数有3个,
则t=1且t<1,当t=1时,g(1)=1+
| 1 |
| 4 |
| 5 |
| 4 |
故答案为:
| 5 |
| 4 |
点评:本题主要考查函数的图象和应用,利用函数和方程之间的关系,作出两个函数的图象是解决本题的关键,综合性较强,难度较大.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
同时具有性质“(1)最小正周期是π;(2)图象关于直线x=
对称;(3)在[
,
]上是减函数”的一个函数可以是( )
| π |
| 6 |
| π |
| 6 |
| π |
| 3 |
A、y=sin(
| ||||
B、y=sin(2x-
| ||||
C、y=cos(2x+
| ||||
D、y=sin(2x+
|
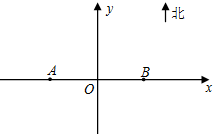 为了监测某海域的船舶航行情况,在该海域设立了如图所示东西走向,相距20海里的A,B两个观测站,观测范围是到A,B两观测站距离之和不超过40海里的区域.
为了监测某海域的船舶航行情况,在该海域设立了如图所示东西走向,相距20海里的A,B两个观测站,观测范围是到A,B两观测站距离之和不超过40海里的区域.