题目内容
下列命题中所有正确的序号是 .
①函数f(x)=x2-2x+a在区间(-2,0)和(2,3)内各有一个零点,则-3<a<0;
②已知f(x)=
对任意x1≠x2都有
>0,那么实数a的范围是1<a<2;
③用min{a,b,c}表示a,b,c三个数中的最小值.设f(x)=min{2x,x+2,10-x}(x≥0),则f(x)的最大值为6;
④若函数y=loga(x2-ax+2)在区间(-∞,1]上为减函数,则a≥2.
①函数f(x)=x2-2x+a在区间(-2,0)和(2,3)内各有一个零点,则-3<a<0;
②已知f(x)=
|
| f(x1)-f(x2) |
| x1-x2 |
③用min{a,b,c}表示a,b,c三个数中的最小值.设f(x)=min{2x,x+2,10-x}(x≥0),则f(x)的最大值为6;
④若函数y=loga(x2-ax+2)在区间(-∞,1]上为减函数,则a≥2.
考点:命题的真假判断与应用
专题:数形结合,分类讨论,函数的性质及应用
分析:①利用二次函数的图象与性质和函数零点的存在定理可得;
②根据题意知,f(x)是增函数,从而求出a的取值范围;
③根据题意,画出函数y=10-x,y=x+2和y=2x的图象,得出f(x)的图象,得到f(x)的最大值;
④根据题意,设g(x)=x2-ax+2(a>0,且a≠1),讨论a的取值,得出满足条件的a的取值范围.
②根据题意知,f(x)是增函数,从而求出a的取值范围;
③根据题意,画出函数y=10-x,y=x+2和y=2x的图象,得出f(x)的图象,得到f(x)的最大值;
④根据题意,设g(x)=x2-ax+2(a>0,且a≠1),讨论a的取值,得出满足条件的a的取值范围.
解答:
解:①∵函数f(x)=x2-2x+a在区间 (-2,0)与(2,3)上各有一个零点,
∴
,
即
,
解得-3<a<0;
∴命题①正确.
②根据题意知,f(x)是增函数,
∴
,
解得
<a<2;
∴命题②不正确.
③根据题意,在同一坐标系中画出函数y=10-x,y=x+2和y=2x的图象,如图;

y=x+2 与y=2x交点是A、B,y=x+2与 y=10-x的交点为C(4,6),
由上图得出f(x)的图象如下:

C为最高点,且C(4,6),所以f(x)的最大值为6;
∴命题③正确.
④根据题意,设g(x)=x2-ax+2(a>0,且a≠1),
当a>1时,g(x)在(-∞,1]上为减函数,
∴
∴2≤a<3;
当0<a<1时,g(x)在(-∞,1]上为减函数,不合题意;
∴2≤a<3;
∴命题④不正确.
故答案为:①③.
∴
|
即
|
解得-3<a<0;
∴命题①正确.
②根据题意知,f(x)是增函数,
∴
|
解得
| 3 |
| 2 |
∴命题②不正确.
③根据题意,在同一坐标系中画出函数y=10-x,y=x+2和y=2x的图象,如图;

y=x+2 与y=2x交点是A、B,y=x+2与 y=10-x的交点为C(4,6),
由上图得出f(x)的图象如下:

C为最高点,且C(4,6),所以f(x)的最大值为6;
∴命题③正确.
④根据题意,设g(x)=x2-ax+2(a>0,且a≠1),
当a>1时,g(x)在(-∞,1]上为减函数,
∴
|
当0<a<1时,g(x)在(-∞,1]上为减函数,不合题意;
∴2≤a<3;
∴命题④不正确.
故答案为:①③.
点评:本题考查了函数的概念、图象、最值、单调性以及零点的问题,也考查了分类讨论思想和数形结合的方法,是综合性题目.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
设x为任意实数,则下列各式正确的是( )
| A、tan(arctanx)=x |
| B、arcsin(sinx)=x |
| C、sin(arcsinx)=x |
| D、cos(arccosx)=x |
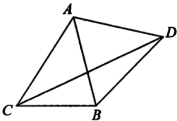 如图,△ABC中.角A、B、C所对边的长分别为a、b、c满足c=l,a2+b2=ab+1,以AB为边向△ABC外作等边三角形△ABD.
如图,△ABC中.角A、B、C所对边的长分别为a、b、c满足c=l,a2+b2=ab+1,以AB为边向△ABC外作等边三角形△ABD.