题目内容
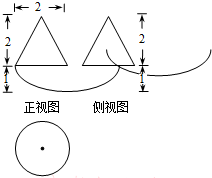
如图是一个空间几何体的三视图，如果直角三角形边长均为1，那么几何体体积为（ ）
| A、1 | ||
B、
| ||
C、
| ||
D、
|
考点：由三视图求面积、体积
专题：计算题,空间位置关系与距离
分析：首先三视图复原的几何体的形状以及特征，结合三视图的数据，求出几何体的体积．
解答：
解：由三视图可知几何体是底面为正方形，一条侧棱垂直底面的四棱锥，
底面正方形的边长为：1，棱锥的高为：1，
所以几何体的体积是：
×1×1×1=
．
故选：B
底面正方形的边长为：1，棱锥的高为：1，
所以几何体的体积是：
| 1 |
| 3 |
| 1 |
| 3 |
故选：B
点评：本题考查几何体的三视图的画法，三视图复原几何体的特征，考查计算能力，空间想象能力，正确求出外接球的半径是解题的关键．
练习册系列答案
相关题目
已知等比数列{an}的公比q＜0，其前n 项的和为Sn，则a9S8与a8S9 的大小关系是（ ）
| A、a9S8＞a8S9 |
| B、a9S8＜a8S9 |
| C、a9S8≥a8S9 |
| D、a9S8≤a8S9 |
如图，四面体ABCD中，平面ABC⊥平面BCD，AC=AB，CB=CD，∠DCB=120°，点E在BD上，且CE=DE．
如图，在直三棱柱ABC-A1B1C1，中，AC=BC=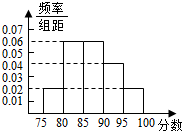
某市教育局为了了解高三学生体育达标情况，在某学校的高三学生体育达标成绩中随机抽取50个进行调研，按成绩分组：第l组[75，80），第2组[80，85），第3组[85，90），第4组[90，95），第5组[95，100]得到的频率分布直方图如图所示：若要在成绩较高的第3，4，5组中用分层抽样抽取6名学生进行复查：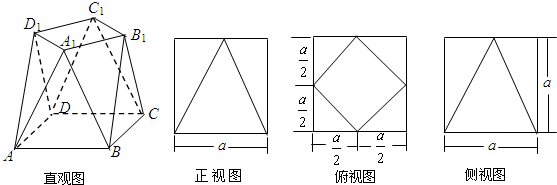
学校为测评班级学生对任课教师的满意度，采用“100分制”打分的方式来计分．现从某班学生中随机抽取10名，以下茎叶图记录了他们对某教师的满意度分数（以十位数字为茎，个位数字为叶）：