题目内容
已知数列数列{an}的通项公式an=(-1)n(2n-1)(n∈N*),Sn为其前n项和
(1)求S1,S2,S3,S4的值;
(2)猜想Sn的表达式,并用数学归纳法证明你的结论.
(1)求S1,S2,S3,S4的值;
(2)猜想Sn的表达式,并用数学归纳法证明你的结论.
考点:数学归纳法,归纳推理
专题:综合题,点列、递归数列与数学归纳法
分析:(1)根据an=(-1)n(2n-1),可求S1,S2,S3,S4的值;
(2)由(1)猜想Sn的表达式,再根据数学归纳法的证题步骤进行证明.
(2)由(1)猜想Sn的表达式,再根据数学归纳法的证题步骤进行证明.
解答:
解:(1)依题设可得S1=-1,S2=-1+3=2,S3=-1+3-5=-3,S4=-1+3-5+7=4;(5分)
(2)猜想:Sn=(-1)n•n.…(7分)
证明:①当n=1时,猜想显然成立.
②假设n=k时,猜想成立,即Sk=(-1)k•k.
那么,当n=k+1时,Sk+1=(-1)k•k+ak+1=(-1)k•k+(-1)k+1(2k+1)=(-1)k+1•(k+1).
即n=k+1时,猜想也成立.
故由①和②,可知猜想成立.…(12分)
(2)猜想:Sn=(-1)n•n.…(7分)
证明:①当n=1时,猜想显然成立.
②假设n=k时,猜想成立,即Sk=(-1)k•k.
那么,当n=k+1时,Sk+1=(-1)k•k+ak+1=(-1)k•k+(-1)k+1(2k+1)=(-1)k+1•(k+1).
即n=k+1时,猜想也成立.
故由①和②,可知猜想成立.…(12分)
点评:本题考查数列的性质和应用,第(1)问要注意递推公式的灵活运用,第二问要注意数学归纳法的证明技巧.

练习册系列答案
相关题目
△ABC的内角A、B、C所对的边分别为a,b,c.若B=2A,a=1,b=
,则这样的三角形有( )
| 2 |
| A、只有一个 | B、有两个 |
| C、不存在 | D、无数个 |
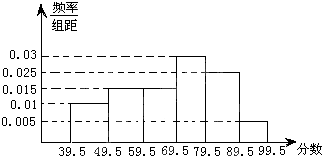 如图,从参加环保知识竞赛的学生中抽出60名,将其成绩(均为整数)整理后画出的频率分布直方图如图所示,观察图形,回答下列问题:
如图,从参加环保知识竞赛的学生中抽出60名,将其成绩(均为整数)整理后画出的频率分布直方图如图所示,观察图形,回答下列问题: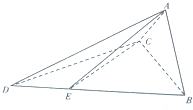 如图,四面体A-BCD中,平面ABC⊥平面BCD,AC=AB,CB=CD,∠DCB=120°.点E在BD上,且DE=
如图,四面体A-BCD中,平面ABC⊥平面BCD,AC=AB,CB=CD,∠DCB=120°.点E在BD上,且DE=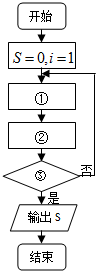 画出一个计算1+
画出一个计算1+