题目内容
已知复数z满足:|z|=1+3i-z
(1)求复数z;
(2)求
的值.
(1)求复数z;
(2)求
| (1+i)2(2+4i)2 |
| 2z |
考点:复数代数形式的混合运算
专题:数系的扩充和复数
分析:(1)设复数z=a+bi,a,b∈R,代入已知式子可得ab的方程组,解方程组可得;(2)把(1)解出的z代入要求解的式子,化简可得.
解答:
解:(1)设复数z=a+bi,a,b∈R,
∵|z|=1+3i-z,∴|z|+z=1+3i,
∴
+a+bi=1+3i,
∴
,解得
,
∴复数z=-4+3i;
(2)
=
=
=
=
.
∵|z|=1+3i-z,∴|z|+z=1+3i,
∴
| a2+b2 |
∴
|
|
∴复数z=-4+3i;
(2)
| (1+i)2(2+4i)2 |
| 2z |
| (1+i)2(2+4i)2 |
| 2(-4+3i) |
=
| 2i•4(-3+4i) |
| 2(-4+3i) |
| 4i•(-3+4i)(-4-3i) |
| (-4+3i)(-4-3i) |
=
| 28+96i |
| 25 |
点评:本题考查复数代数形式的混合运算,属基础题.

练习册系列答案
相关题目
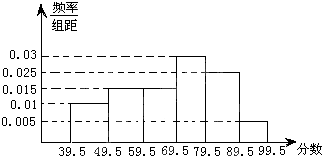 如图,从参加环保知识竞赛的学生中抽出60名,将其成绩(均为整数)整理后画出的频率分布直方图如图所示,观察图形,回答下列问题:
如图,从参加环保知识竞赛的学生中抽出60名,将其成绩(均为整数)整理后画出的频率分布直方图如图所示,观察图形,回答下列问题: 如图,四棱锥P-ABCD中,四边形ABCD为矩形,平面PAD⊥平面ABCD,且E、O分别为PC、BD的中点.求证:
如图,四棱锥P-ABCD中,四边形ABCD为矩形,平面PAD⊥平面ABCD,且E、O分别为PC、BD的中点.求证: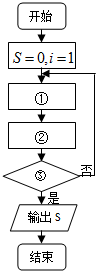 画出一个计算1+
画出一个计算1+ 某班50位学生期中考试数学成绩的频率分布直方图如图所示,其中成绩分组区间是:[40,50)、[50,60)、[60,70)、[70,80)、[90,100)、[90,100].
某班50位学生期中考试数学成绩的频率分布直方图如图所示,其中成绩分组区间是:[40,50)、[50,60)、[60,70)、[70,80)、[90,100)、[90,100].