题目内容
在△ABC中，内角A，B，C的对边分别为a，b，c，S为该三角形的面积，且2sinB-2sin2B-cos2B=
-1．
（Ⅰ）求角B的大小；
（Ⅱ）若B为锐角，a=6，S=6
，求b的值．
| 3 |
（Ⅰ）求角B的大小；
（Ⅱ）若B为锐角，a=6，S=6
| 3 |
考点：余弦定理,正弦定理
专题：三角函数的求值
分析：（Ⅰ）已知等式利用二倍角的余弦函数公式化简，整理求出sinB的值，即可确定出角B的大小；
（Ⅱ）由B为锐角确定出B的度数，利用三角形面积公式列出关系式，将a，S，以及sinB的值代入求出c的值，再由a，c，cosB的值，利用余弦定理即可求出b的值．
（Ⅱ）由B为锐角确定出B的度数，利用三角形面积公式列出关系式，将a，S，以及sinB的值代入求出c的值，再由a，c，cosB的值，利用余弦定理即可求出b的值．
解答：
解：（Ⅰ）2sinB-2sin2B-cos2B=2sinB-2sin2B-（1-2sin2B）=
-1，即2sinB-1=
-1，
∴sinB=
，
则B=
或
；
（Ⅱ）∵B为锐角，∴B=
，
∵S=
acsinB，a=6，sinB=
，S=6
，
∴
×6c×
=6
，
解得：c=4，
由余弦定理得：b2=a2+c2-2accosB=36+16-24=28，
则b=2
．
| 3 |
| 3 |
∴sinB=
| ||
| 2 |
则B=
| π |
| 3 |
| 2π |
| 3 |
（Ⅱ）∵B为锐角，∴B=
| π |
| 3 |
∵S=
| 1 |
| 2 |
| ||
| 2 |
| 3 |
∴
| 1 |
| 2 |
| ||
| 2 |
| 3 |
解得：c=4，
由余弦定理得：b2=a2+c2-2accosB=36+16-24=28，
则b=2
| 7 |
点评：此题考查了正弦、余弦定理，以及特殊角的三角函数值，熟练掌握定理是解本题的关键．
练习册系列答案
相关题目
复数i3的值是（ ）
| A、-i | B、1 | C、-1 | D、i |
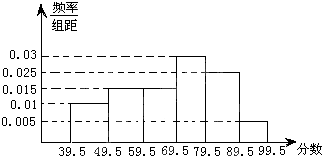如图，从参加环保知识竞赛的学生中抽出60名，将其成绩（均为整数）整理后画出的频率分布直方图如图所示，观察图形，回答下列问题：
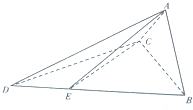如图，四面体A-BCD中，平面ABC⊥平面BCD，AC=AB，CB=CD，∠DCB=120°．点E在BD上，且DE=
如图，四棱锥P-ABCD中，四边形ABCD为矩形，平面PAD⊥平面ABCD，且E、O分别为PC、BD的中点．求证：