题目内容
 外国油轮(简称外轮)除特许外,不得进入离我国海岸线12海里以内的区域.如图所示,我国某海岛是由半径为10海里的一段圆弧
外国油轮(简称外轮)除特许外,不得进入离我国海岸线12海里以内的区域.如图所示,我国某海岛是由半径为10海里的一段圆弧 |
| ABC |
| 3 |
| 4 |
(1)该外轮是否已进入我国领海主权范围内?
(2)该外轮因故障向我方求助,我方停泊在A处的求助船紧急起航,首先沿正北方向AN行驶一段至点M位置,再从M(“拐点”)向右拐头沿直线MP前往出事点,记“拐角”∠NMP的大小为θ.由于水域的原因,救助船沿AN方向的行船最大速度是MP方向行船最大速度的λ倍.试确定cosθ的值,使我方救助船到达P点的时间最短.
考点:解三角形的实际应用
专题:解三角形
分析:(1)连接OP,根据已知条件求得∠APB,求得OP,跟22比较大小即可.
(2)作PQ⊥AN于Q,PS⊥AB于S,确定∠NMP=θ,设MP方向的船速为V,表示出我救助船全速到达P点共所需时间,令T′(θ)=0求得cosθ,利用导函数与0的比较确定此时cosθ最小值,另一方面,延长PC与AN交于M0,须QM0≥QM救助船才能沿直线MP航行根据cosθ≤cos∠QM0P,求得λ的范围,最后综合求得cosθ.
(2)作PQ⊥AN于Q,PS⊥AB于S,确定∠NMP=θ,设MP方向的船速为V,表示出我救助船全速到达P点共所需时间,令T′(θ)=0求得cosθ,利用导函数与0的比较确定此时cosθ最小值,另一方面,延长PC与AN交于M0,须QM0≥QM救助船才能沿直线MP航行根据cosθ≤cos∠QM0P,求得λ的范围,最后综合求得cosθ.
解答:
解:(1)连接OP,因∠BAP=30°,∠ABP=120°,
∴∠APB=30°.
在△PBO中,OP2=102+202-2×10×20cos120°=700OP2>(10+12)2,即OP>22,故该外轮未进入我领海主权范围内.
(2)作PQ⊥AN于Q,PS⊥AB于S,则AQ=SP=10
,PQ=30,
因∠NAP=60°,∠NMP=θ,首先应有θ>60°,PM=
,AM=10
-
,
设MP方向的船速为V,则我救助船全速到达P点共所需时间为T(θ)=
(10
-
)+
•
=
+
×
,
T′(θ)=
×
,令T′(θ)=0得cosθ=
,设使cosθ=
的锐角为θλ,在当θ∈(60°,θλ)时,T'(θ)<0,当θ∈(θλ,90°)时,T'(θ)>0;T(θ)在(60°,θλ)上递减,在(θλ,90°)上递增,
所以当cosθ=
时,T(θ)取得最小值.
另一方面,延长PC与AN交于M0,须QM0≥QM救助船才能沿直线MP航行,cosθ≤cos∠QM0P=
=
,
由
≤
解得λ≥
,此时θλ≥∠QM0P,而当λ<
时,θλ<∠QM0P,
由T(θ)的单调性知θ取∠QM0P时,T(θ)最小.
综上可知,为使到达P点时间最短,当λ≥
时,救助船选择的拐角θ应满足cosθ=
;当λ<
时,救助船应在M0处拐头直朝P点航行,此时cosθ=
.
∴∠APB=30°.
在△PBO中,OP2=102+202-2×10×20cos120°=700OP2>(10+12)2,即OP>22,故该外轮未进入我领海主权范围内.
(2)作PQ⊥AN于Q,PS⊥AB于S,则AQ=SP=10
| 3 |
因∠NAP=60°,∠NMP=θ,首先应有θ>60°,PM=
| 30 |
| sinθ |
| 3 |
| 30cosθ |
| sinθ |
设MP方向的船速为V,则我救助船全速到达P点共所需时间为T(θ)=
| 1 |
| λV |
| 3 |
| 30cosθ |
| sinθ |
| 1 |
| V |
| 30 |
| sinθ |
10
| ||
| λV |
| 30 |
| λV |
| λ-cosθ |
| sinθ |
T′(θ)=
| 30 |
| λV |
| 1-λcosθ |
| sin2θ |
| 1 |
| λ |
| 1 |
| λ |
所以当cosθ=
| 1 |
| λ |
另一方面,延长PC与AN交于M0,须QM0≥QM救助船才能沿直线MP航行,cosθ≤cos∠QM0P=
10
| ||||
|
| ||||
|
由
| 1 |
| λ |
| ||||
|
5+2
|
5+2
|
由T(θ)的单调性知θ取∠QM0P时,T(θ)最小.
综上可知,为使到达P点时间最短,当λ≥
5+2
|
| 1 |
| λ |
5+2
|
| ||||
|
点评:本题主要考查了解三角形的实际应用.考查了学生分析推理和解决实际问题的能力.

练习册系列答案
相关题目
已知某随机变量X的分布如下(p,q∈R)
且X的数学期望E(X)=
,那么X的方差D(X)等于( )
| X | 1 | -1 |
| P | p | q |
| 1 |
| 2 |
A、
| ||
B、
| ||
C、
| ||
| D、1 |
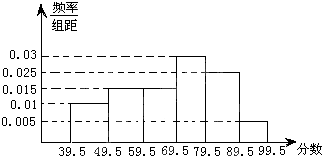 如图,从参加环保知识竞赛的学生中抽出60名,将其成绩(均为整数)整理后画出的频率分布直方图如图所示,观察图形,回答下列问题:
如图,从参加环保知识竞赛的学生中抽出60名,将其成绩(均为整数)整理后画出的频率分布直方图如图所示,观察图形,回答下列问题:
 某班50位学生期中考试数学成绩的频率分布直方图如图所示,其中成绩分组区间是:[40,50)、[50,60)、[60,70)、[70,80)、[90,100)、[90,100].
某班50位学生期中考试数学成绩的频率分布直方图如图所示,其中成绩分组区间是:[40,50)、[50,60)、[60,70)、[70,80)、[90,100)、[90,100].