Question

8．如图，在四棱锥P-ABCD中，底面ABCD为直角梯形，AD∥BC，AD⊥DC，平面PAD⊥底面ABCD，Q为AD中点，M是棱PC的中点．△PAD是边长为2的正三角形，BC=1，CD=$\sqrt{3}$．
（1）求证：平面PQB⊥平面PAD；
（2）求二面角M-BQ-C平面角θ的大小．

Answer 1

分析 （1）推导出四边形BCDQ为平行四边形，从而CD∥BQ，QB⊥AD，进而BQ⊥平面PAD，由此能证明平面PQB⊥平面PAD．
（2）连接CQ，BD交于一点H，连接MH，则MH∥PQ，取QB中点N，连接MN，NH，则QB⊥平面MHN，∠MNH为所求角θ，由此能出二面角M-BQ-C平面角θ的大小．

解答 证明：（1）∵AD∥BC，$BC=\frac{1}{2}AD$，Q为AD的中点，则BC=QD，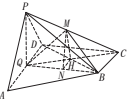
∴四边形BCDQ为平行四边形，∴CD∥BQ．（2分）
∵AD⊥DC，∴QB⊥AD，
又∵平面PAD⊥平面ABCD，且平面PAD∩平面ABCD=AD．（4分）
∴BQ⊥平面PAD．
∵BQ?平面PQB，∴平面PQB⊥平面PAD．（6分）
解：（2）连接CQ，BD交于一点H，连接MH，则MH是△PCQ的中位线，
∴MH∥PQ，
∵PA=PD，Q为AD的中点，∴PQ⊥AD，
又∵平面PAD⊥平面ABCD，且平面PAD∩平面ABCD=AD，
∴PQ⊥平面ABCD，∴MH⊥平面QBC，∴MH⊥QB．（8分）
取QB中点N，连接MN，NH，
又∵NH是△QBC的中位线，∴NH∥BC，
∴NH⊥QB，则QB⊥平面MHN，∴∠MNH为所求角θ，
在RT△MNH中，$NH=\frac{1}{2}BC=\frac{1}{2}$，$MH=\frac{1}{2}PQ=\frac{{\sqrt{3}}}{2}$，
∴$tanθ=\frac{MH}{NH}=\sqrt{3}$，∵θ∈（0，π），∴$θ=\frac{π}{3}$．
∴二面角M-BQ-C平面角θ的大小为$\frac{π}{3}$．（12分）

点评 本题考查面面垂直的证明，考查二面角的大小的求法，是中档题，解题时要认真审题，注意空间思维能力的培养．