题目内容
1．某三棱锥的三视图如图所示，正视图是边长为3的等边三角形，则该三棱锥外接球的表面积为（ ）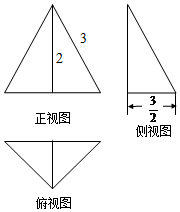
| A． | 12π | B． | $6\sqrt{3}π$ | C． | 9π | D． | 18π |
分析 根据题意得到该几何体有一个侧面PAC垂直于底面，高为$\frac{3\sqrt{3}}{2}$，底面是一个等腰直角三角形的三棱锥，如图所示，这个几何体的外接球的球心O在高线PD上，且是等边三角形PAC的中心，求出外接球的半径，即可确定出表面积．
解答 
解：由已知中正视图是一个正三角形，侧视图和俯视图均为三角形，
可得该几何体是有一个侧面PAC垂直于底面，高为$\frac{3\sqrt{3}}{2}$，底面是一个等腰直角三角形的三棱锥，如图所示，
∴这个几何体的外接球的球心O在高线PD上，且是等边三角形PAC的中心，
∴这个几何体的外接球的半径R=$\frac{2}{3}$PD=$\sqrt{3}$，
则几何体的外接球的表面积为4πR2=12π．
故选A．
点评 此题考查了由三视图求面积、体积，根据三视图正确画出几何体是解本题的关键．
练习册系列答案
相关题目
16．函数f（x）=x2-ax-1在区间（-$\frac{1}{2}$，$\frac{1}{2}$）上有零点，则实数a的取值范围是（ ）
| A． | （$\frac{3}{2}$，+∞） | B． | （-∞，-$\frac{3}{2}$） | C． | （-∞，-$\frac{3}{2}$）∪（$\frac{3}{2}$，+∞） | D． | （-$\frac{3}{2}$，$\frac{3}{2}$） |
6．下列命题中为真命題的是（ ）
| A． | 命题“若x＞1，则x2＞1”的逆命题 | B． | 命题“若x=1，则x2+x-2=0”的否命题 | ||
| C． | 命题“若x＞y，则x＞|y|”的逆命题 | D． | 命题“若x2＞0，则x＞-1”的逆否命题 |
13．角θ的终边过点（sin（α-$\frac{π}{3}$），$\sqrt{3}$），且sin2θ≤0，则α的可能取值范围是（ ）
| A． | [-$\frac{2π}{3}$，$\frac{π}{3}$] | B． | [$\frac{π}{3}$，$\frac{4π}{3}$] | C． | [-$\frac{5π}{3}$，-$\frac{2π}{3}$] | D． | [0，π] |
10．等差数列{an}，{bn}的前n项和分别为Sn，Tn，若$\frac{{S}_{n}}{{T}_{n}}$=$\frac{2n}{3n+1}$，则$\frac{{a}_{4}+{a}_{6}}{{b}_{3}+{b}_{7}}$=（ ）
| A． | $\frac{2}{3}$ | B． | $\frac{14}{9}$ | C． | $\frac{9}{14}$ | D． | $\frac{3}{2}$ |