题目内容
已知函数f(x)=(cos2xcosx+sin2xsinx)sinx,x∈R,则函数f(x)性质的以下判断中正确的是( )
A、函数f(x)的最小正周期为
| ||||
B、函数f(x)的单调增区间是[kπ-
| ||||
C、函数f(x)的图象关于点(
| ||||
D、函数g(x)=f(x-
|
考点:函数y=Asin(ωx+φ)的图象变换,三角函数中的恒等变换应用
专题:三角函数的图像与性质
分析:利用两角差的余弦化简f(x),求周期判断A;利用复合函数的单调性求增区间判断B,代入x=
判断C;求出函数g(x),代入x=
判断D.
| π |
| 6 |
| π |
| 12 |
解答:
解:∵f(x)=(cos2xcosx+sin2xsinx)sinx
=cos(2x-x)sinx=cosxsinx=
sin2x.
∴函数f(x)的最小正周期为π.选项A错误;
由-
+2kπ≤2x≤
+2kπ,得kπ-
≤x≤kπ+
,k∈Z.
∴函数f(x)的单调增区间是[kπ-
,kπ+
],k∈Z.选项B错误;
∵f(
)=
sin2×
=
.选项C错误;
g(x)=f(x-
)=
sin2(x-
)=
sin(2x-
).
又g(
)=
sin(2×
-
)=-
.
∴函数g(x)=f(x-
)的图象关于直线x=
对称.
故选:D.
=cos(2x-x)sinx=cosxsinx=
| 1 |
| 2 |
∴函数f(x)的最小正周期为π.选项A错误;
由-
| π |
| 2 |
| π |
| 2 |
| π |
| 4 |
| π |
| 4 |
∴函数f(x)的单调增区间是[kπ-
| π |
| 4 |
| π |
| 4 |
∵f(
| π |
| 6 |
| 1 |
| 2 |
| π |
| 6 |
| ||
| 4 |
g(x)=f(x-
| π |
| 3 |
| 1 |
| 2 |
| π |
| 3 |
| 1 |
| 2 |
| 2π |
| 3 |
又g(
| π |
| 12 |
| 1 |
| 2 |
| π |
| 12 |
| 2π |
| 3 |
| 1 |
| 2 |
∴函数g(x)=f(x-
| π |
| 3 |
| π |
| 12 |
故选:D.
点评:本题考查了y=Asin(ωx+φ)型函数的图象和性质,考查了两角和的余弦公式,是中档题.

练习册系列答案
 课时训练江苏人民出版社系列答案
课时训练江苏人民出版社系列答案 黄冈经典趣味课堂系列答案
黄冈经典趣味课堂系列答案 启东小题作业本系列答案
启东小题作业本系列答案
相关题目
化简
-
-
+
得( )
| AC |
| AB |
| BD |
| CD |
A、
| ||
B、
| ||
C、
| ||
D、
|
平面向量
与
的夹角为
,
=(3,0),|
|=2,则|
+2
|═( )
| a |
| b |
| 2π |
| 3 |
| a |
| b |
| a |
| b |
A、
| ||
B、
| ||
| C、7 | ||
| D、3 |
设集合U={1,2,3,4,5},A={1,3,5},B={2,3,5},则图中阴影部分表示的集合是( )
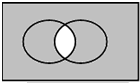

| A、{1,2,4} | B、{4} |
| C、{3,5} | D、∅ |
已知全集M={x||2x-1|≤1,x∈Z},集合N={3,a},若M∩N≠∅,则a等于( )
| A、1 | B、2 | C、1或2 | D、0或1 |
