题目内容
4.函数y=$\frac{{x}^{2}ln|x|}{|x|}$的图象大致是( )| A. | 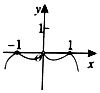 | B. | 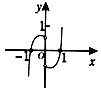 | C. | 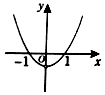 | D. | 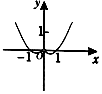 |
分析 判断函数的奇偶性,排除选项,利用函数经过的特殊点,以及特殊函数的值,判断函数的单调性,然后判断函数的图象即可.
解答 解:函数y=$\frac{{x}^{2}ln|x|}{|x|}$是偶函数,所以选项B错误,第x=e时,y=e,所以选项A,错误;
当x∈(0,1)时,y=xlnx,y′=lnx+1,x=$\frac{1}{e}$时,y′=0,0<x<$\frac{1}{e}$,y′<0,函数是减函数,$\frac{1}{e}$<x<1,y′>0,函数是增函数.
所以C错误.
故选:D.
点评 本题考查函数的图象的判断,函数的奇偶性,单调性,特殊点,往往是判断函数的图象的方法,考查转化思想以及计算能力.

练习册系列答案
相关题目
12.任意a∈R,曲线y=ex(x2+ax+1-2a)在点P(0,1-2a)处的切线l与圆C:x2+2x+y2-12=0的位置关系是( )
| A. | 相交 | B. | 相切 | C. | 相离 | D. | 以上均有可能 |
13.已知F1,F2分别是双曲线$\frac{y^2}{a^2}-\frac{x^2}{b^2}=1(a,b>0)$的两个焦点,过其中一个焦点与双曲线的一条渐近线平行的直线交双曲线另一条渐近线于点M,若点M在以线段F1F2为直径的圆内,则双曲线离心率的取值范围是( )
| A. | (1,2) | B. | (2,+∞) | C. | $(1,\;\sqrt{2})$ | D. | $(\sqrt{2},\;+∞)$ |
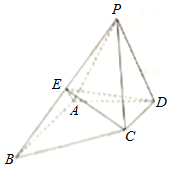 如图,四棱锥P-ABCD中,△PAD为正三角形,AB∥CD,AB=2CD,∠BAD=90°,PA⊥CD,E为棱PB的中点
如图,四棱锥P-ABCD中,△PAD为正三角形,AB∥CD,AB=2CD,∠BAD=90°,PA⊥CD,E为棱PB的中点