题目内容
9.已知数列{an}是等差数列,其首项为2,且公差为2,若${b_n}={2^{a_n}}$(n∈N*).(1)求证:数列{bn}是等比数列;
(2)设cn=an+bn,求数列{cn}的前n项和An.
分析 (Ⅰ)等差数列{an}的通项an=2+(n-1)×2=2n,bn=22n,$\frac{{b}_{n+1}}{{b}_{n}}=\frac{{2}^{2(n+1)}}{{2}^{2n}}=4$;
(2)cn=an+bn=2n+4n,分组求和即可.
解答 解:(1)证明:因为等差数列{an}的首项和公差都为2,
所以an=2+(n-1)×2=2n,
又因为bn=22n,
所以$\frac{{b}_{n+1}}{{b}_{n}}=\frac{{2}^{2(n+1)}}{{2}^{2n}}=4$,
所以数列{bn}是以4为首项和公比的等比数列; …(8分)
(2)解:因为cn=an+bn=2n+4n,
等差数列{an}的前n项和sn=$\frac{2+2n}{2}•n=n(n+1)$,
等比数列{bn}的前n项和Tn=$\frac{4(1-{4}^{n})}{1-4}=\frac{4}{3}({4}^{n}-1)$
所以{cn}的前n项和An=sn+Tn=n(n+1)+$\frac{4}{3}({4}^{n}-1)$.…(13分)
点评 本题考查了等差数列、等比数列的计算,及分组求和,属于中档题.

练习册系列答案
相关题目
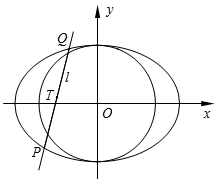 在平面直角坐标系xOy中,已知圆O:x2+y2=b2经过椭圆$E:\frac{x^2}{4}+\frac{y^2}{b^2}=1$(0<b<2)的焦点.
在平面直角坐标系xOy中,已知圆O:x2+y2=b2经过椭圆$E:\frac{x^2}{4}+\frac{y^2}{b^2}=1$(0<b<2)的焦点.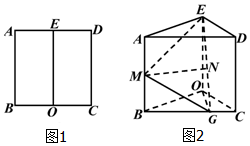 如图1,在边长为$2\sqrt{3}$的正方形ABCD中,E、O分别为 AD、BC的中点,沿 EO将矩形ABOE折起使得∠BOC=120°,如图2,点G 在BC上,BG=2GC,M、N分别为AB、EG中点.
如图1,在边长为$2\sqrt{3}$的正方形ABCD中,E、O分别为 AD、BC的中点,沿 EO将矩形ABOE折起使得∠BOC=120°,如图2,点G 在BC上,BG=2GC,M、N分别为AB、EG中点.