题目内容

15．已知函数f（x）=xlnx+ax2-1，且f'（1）=-1．
（1）求a的值；
（2）若对于任意x∈（0，+∞），都有f（x）-mx≤-1，求m的最小值．

分析 （1）求出导数，利用f'（1）=-1，求解即可．
（2）设g（x）=lnx-x，则$g'（x）=\frac{1}{x}-1$，判断函数的单调性，求出最值即可得到结果．

解答 解：（1）对f（x）求导，得f'（x）=1+lnx+2ax，
所以f'（1）=1+2a=-1，解得a=-1．
（2）由f（x）-mx≤-1，得xlnx-x2-mx≤0，
因为x∈（0，+∞），所以对于任意x∈（0，+∞），都有lnx-x≤m．
设g（x）=lnx-x，则$g'（x）=\frac{1}{x}-1$，
令g'（x）=0，解得x=1，
当x变化时，g（x）与g'（x）的变化情况如下表：

x（0，1）1（1，+∞）
g'（x）+0-
g（x）增极大值减
所以当x=1时，g（x）max=g（1）=-1，
因为对于任意x∈（0，+∞），都有g（x）≤m成立，所以m≥-1，
所以m的最小值为-1．

点评 本题考查函数的导数的应用，函数的最值的求法，考查转化思想以及计算能力．

练习册系列答案
相关题目
5．已知cosα，sinα是函数f（x）=x2-tx+t（t∈R）的两个零点，则sin2α=（　　）
A．2-2$\sqrt{2}$B．2$\sqrt{2}$-2C．$\sqrt{2}$-1D．1-$\sqrt{2}$
6．已知函数$f（x）=\left\{\begin{array}{l}{2^x}，x≤3\\{log_2}x，x＞3\end{array}\right.$，则f（f（3））=3．
3．已知函数f（x）的定义域为D，若存在区间[m，n]⊆D使得f（x）：
（Ⅰ）f（x）在[m，n]上是单调函数；
（Ⅱ）f（x）在[m，n]上的值域是[2m，2n]，
则称区间[m，n]为函数f（x）的“倍值区间”．
下列函数中存在“倍值区间”的有①②④（填上所有你认为正确的序号）
①f（x）=x2； ②$f（x）=\frac{1}{x}$；③$f（x）=x+\frac{1}{x}$；   ④$f（x）=\frac{3x}{{{x^2}+1}}$．
10．已知函数f（x）是定义在R上的偶函数，且在区间[0，+∞）上单调递增，若实数b满足$2f（{log_2}b）+f（{log_{\frac{1}{2}}}b）≤3f（1）$，则实数b的取值范围是$[{\frac{1}{2}，2}]$．
20．设集合A={1，3，5，7}，B={2，3，4}，则A∩B={3}．
7．设等比数列{an}的公比为q，前n项和为Sn，则“|q|=1”是“S6=3S2”的（　　）
A．充分不必要条件B．必要不充分条件
C．充要条件D．既不充分也不必要条件
4．函数y=$\frac{{x}^{2}ln|x|}{|x|}$的图象大致是（　　）
A．B．C．D．
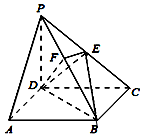5．如图，四棱锥P-ABCD的底面ABCD是正方形，侧棱PD⊥底面ABCD，PD=DC=2，E是PC的中点，EF⊥PB交PB于点F．
（Ⅰ）求点C到平面BDE的距离；
（Ⅱ）证明：PB⊥平面DEF．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网