题目内容
已知y=f(x)是奇函数,当x≥0为减函数,f(1+a)<-f(a),则a的取值范围是 .
考点:函数奇偶性的性质
专题:函数的性质及应用
分析:由条件利用奇函数的性质可得函数在R上是减函数,再根据f(1+a)<-f(a)=f(-a),可得 a+1>-a,由此求得a的取值范围.
解答:
解:∵y=f(x)是奇函数,当x≥0为减函数,
∴函数f(x)在x<0也是减函数,故函数在R上是减函数.
再根据f(1+a)<-f(a)=f(-a),可得 a+1>-a,
求得a>
,
故答案为:(
,+∞).
∴函数f(x)在x<0也是减函数,故函数在R上是减函数.
再根据f(1+a)<-f(a)=f(-a),可得 a+1>-a,
求得a>
| 1 |
| 2 |
故答案为:(
| 1 |
| 2 |
点评:本题主要考查奇函数的性质,函数的单调性的应用,属于基础题.

练习册系列答案
 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案
相关题目
要得到函数y=sinx-cosx的图象,只需将函数y=sinx+cosx的图象( )
A、向右平移
| ||
B、向左平移
| ||
| C、向右平移π个单位长度 | ||
| D、向左平移π个单位长度 |
用秦九韶算法计算f(x)=6x5-4x4+x3-2x2-9x-9,需要加法(或减法)与乘法运算的次数分别为( )
| A、5,4 | B、5,5 |
| C、4,4 | D、4,5 |
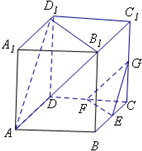 如图,在正方体ABCD=A1B1C1D1中,E、F、G分别是CB、CD、CC1的中点.
如图,在正方体ABCD=A1B1C1D1中,E、F、G分别是CB、CD、CC1的中点.


