题目内容
已知函数f(x)=-(1+λ)x2+2(1-λ)x+1在[-1,1]上是增函数,求实数λ的取值范围.
考点:二次函数在闭区间上的最值
专题:函数的性质及应用
分析:分二次项的系数大于零、等于零、小于零三种情况,分别利用条件以及二次函数的性质,分别求得实数λ的取值范围,再取并集,即得所求.
解答:
解:当-(1+λ)>0,即λ<-1时,应有
≤-1,即
≤0,求得λ<-1,∴λ<-1.
当-(1+λ)=0,即λ=-1时,f(x)=4x+1,满足在[-1,1]上是增函数.
当-(1+λ)<0,即λ>-1时,应有有
≥1,即
≤0,求得λ≤0,∴-1<λ≤0.
综上可得,实数λ的取值范围为(-∞,0].
| 2(1-λ) |
| 2(1+λ) |
| 2 |
| 1+λ |
当-(1+λ)=0,即λ=-1时,f(x)=4x+1,满足在[-1,1]上是增函数.
当-(1+λ)<0,即λ>-1时,应有有
| 2(1-λ) |
| 2(1+λ) |
| 2λ |
| 1+λ |
综上可得,实数λ的取值范围为(-∞,0].
点评:本题主要考查求二次函数在闭区间上的最值,二次函数的性质的应用,体现了分类讨论的数学思想,属基础题.

练习册系列答案
相关题目
设m,n是两条不同的直线,α,β是两个不同的平面,下列命题中正确的是( )
| A、若m∥n,n?α则 m∥α |
| B、若m?α,α⊥β,则m⊥β |
| C、若m∥n,m⊥α,则n⊥α |
| D、若m⊥n,m?α,n?β,则α⊥β |
下列有关命题的说法正确的是( )
| A、命题“若x2=1,则x=1”的否命题为:“若x2=1,则x≠1” |
| B、命题“若x=y,则sinx=siny”的逆否命题为真命题 |
| C、若p∧q为假命题,则p,q均为假命题 |
| D、若关于x的不等式ax2+ax-2<0恒成立,则-8<a<0 |
 如图所示,向量
如图所示,向量 如图,某商业中心O有通往正东方向和北偏东30°方向的两条街道,某公园P位于商业中心北偏东θ角(0<θ<
如图,某商业中心O有通往正东方向和北偏东30°方向的两条街道,某公园P位于商业中心北偏东θ角(0<θ<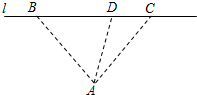 某供货商拟从码头A发货至其对岸l的两个商场B,C处,通常货物先由A处船运至BC之间的中转站D,再利用车辆转运.如图,码头A与两商场B,C的距离相等,两商场间的距离为20千米,且∠BAC=
某供货商拟从码头A发货至其对岸l的两个商场B,C处,通常货物先由A处船运至BC之间的中转站D,再利用车辆转运.如图,码头A与两商场B,C的距离相等,两商场间的距离为20千米,且∠BAC=