题目内容
已知Sn=C
a1+C
a2+…+C
an,n∈N*.
(1)若Sn=n•2n-1(n∈N),是否存在等差数列{an}对一切自然数n满足上述等式?
(2)若数列{an}是公比为q(q≠±1),首项为1的等比数列,数列{bn}满足b1+b2+…+bn=
(n∈N*),求证:{bn}是等比数列.
1 n |
2 n |
n n |
(1)若Sn=n•2n-1(n∈N),是否存在等差数列{an}对一切自然数n满足上述等式?
(2)若数列{an}是公比为q(q≠±1),首项为1的等比数列,数列{bn}满足b1+b2+…+bn=
| Sn |
| 2n |
考点:等比数列的性质
专题:综合题,等差数列与等比数列
分析:(1)设Sn=Cn1+2Cn2+3Cn3+…+nCnn通过倒序相加法得到结论;
(2)求出Sn=
,再利用b1+b2+…+bn=
,求出bn+1,即可证明{bn}是等比数列.
(2)求出Sn=
| (1+q)n |
| q |
| Sn |
| 2n |
解答:
(1)解:an=n(n∈N*).
下面证明:Cn1+2Cn2+3Cn3+…+nCnn=n•2n-1.
设Sn=Cn1+2Cn2+3Cn3+…+nCnn
有Sn=0Cn0+Cn1+2Cn2+3Cn3+…+nCnn
又Sn=nCnn+(n-1)Cnn-1+(n-2)Cnn-2+…+0•Cn0,
两式相加2Sn=n(Cn0+Cn1+Cn2+…+Cnn)=n•2n,
故Sn=n•2n-1,n•2n-1=Cn1+2Cn2+3Cn3+…+nCnn;
(2)证明:∵数列{an}是公比为q(q≠±1),首项为1的等比数列,∴ak=qk-1,
∴Sn=
,
∵b1+b2+…+bn=
,
∴bn+1=
-
=
[(
)n+1-(
)n]=
•(
)n,
∴
=
,
∴{bn}是等比数列.
下面证明:Cn1+2Cn2+3Cn3+…+nCnn=n•2n-1.
设Sn=Cn1+2Cn2+3Cn3+…+nCnn
有Sn=0Cn0+Cn1+2Cn2+3Cn3+…+nCnn
又Sn=nCnn+(n-1)Cnn-1+(n-2)Cnn-2+…+0•Cn0,
两式相加2Sn=n(Cn0+Cn1+Cn2+…+Cnn)=n•2n,
故Sn=n•2n-1,n•2n-1=Cn1+2Cn2+3Cn3+…+nCnn;
(2)证明:∵数列{an}是公比为q(q≠±1),首项为1的等比数列,∴ak=qk-1,
∴Sn=
| (1+q)n |
| q |
∵b1+b2+…+bn=
| Sn |
| 2n |
∴bn+1=
| Sn+1 |
| 2n+1 |
| Sn |
| 2n |
| 1 |
| q |
| 1+q |
| 2 |
| 1+q |
| 2 |
| q-1 |
| 2q |
| 1+q |
| 2 |
∴
| bn+1 |
| bn |
| 1+q |
| 2 |
∴{bn}是等比数列.
点评:本题考查数列的求和,考查等比数列的证明,难点在于对组合数性质的转化与应用,属于难题.

练习册系列答案
 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案
相关题目
已知函数f(x)=lgx,若对任意的正数x,不等式f(x)+f(t)≤f(x2+t)恒成立,则实数t的取值范围是( )
| A、(0,4) |
| B、(1,4] |
| C、(0,4] |
| D、[4,+∞) |
 为了解某年级女生五十米短跑情况,从该年级中随机抽取8名女生进行五十跑测试,她们的测试成绩(单位:秒)的茎叶图(以整数部分为茎,小数部分为叶)如图所示.由此可估计该年级女生五十米跑成绩及格(及格成绩为9.4秒)的概率为( )
为了解某年级女生五十米短跑情况,从该年级中随机抽取8名女生进行五十跑测试,她们的测试成绩(单位:秒)的茎叶图(以整数部分为茎,小数部分为叶)如图所示.由此可估计该年级女生五十米跑成绩及格(及格成绩为9.4秒)的概率为( )| A、0.375 | B、0.625 |
| C、0.5 | D、0.125 |
函数y=f(x)是定义在R上的减函数,且f(1)=0,则满足f(lgx)<0的解集为( )
| A、(0,1) | ||
B、(0,
| ||
| C、(10,+∞) | ||
| D、(1,+∞) |
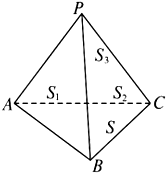 在△ABC中,射影定理可以表示为a=bcosC+ccosB,其中a,b,c依次为角A、B、C的对边.类比以上定理,如图,在四面体P-ABC中,S1、S2、S3、S分别表示△PAB、△PBC、△PCA、△ABC的面积,α、β、γ依次表示面PAB、面PBC、面PCA与底面ABC所成角的大小,我们猜想将射影定理类比推广到三维空间,其表现形式应为
在△ABC中,射影定理可以表示为a=bcosC+ccosB,其中a,b,c依次为角A、B、C的对边.类比以上定理,如图,在四面体P-ABC中,S1、S2、S3、S分别表示△PAB、△PBC、△PCA、△ABC的面积,α、β、γ依次表示面PAB、面PBC、面PCA与底面ABC所成角的大小,我们猜想将射影定理类比推广到三维空间,其表现形式应为 从某小区抽取100个家庭进行月用电量调查,发现其月用电量都在50度至350度之间,频率分布直方图如图所示.
从某小区抽取100个家庭进行月用电量调查,发现其月用电量都在50度至350度之间,频率分布直方图如图所示.