题目内容
已知函数f(x)=lgx,若对任意的正数x,不等式f(x)+f(t)≤f(x2+t)恒成立,则实数t的取值范围是( )
| A、(0,4) |
| B、(1,4] |
| C、(0,4] |
| D、[4,+∞) |
考点:对数函数的图像与性质,函数恒成立问题
专题:函数的性质及应用
分析:若不等式f(x)+f(t)≤f(x2+t)恒成立,则x2-tx+t≥0对任意的正数恒成立,进而根据对数的真数大于0,可得t>0且
≥0,解得答案.
| 4t-t2 |
| 4 |
解答:
解:∵函数f(x)=lgx,
若不等式f(x)+f(t)≤f(x2+t)恒成立,
则x2-tx+t≥0对任意的正数恒成立,
则t>0且
≥0,
解得:t∈(0,4],
故选:C.
若不等式f(x)+f(t)≤f(x2+t)恒成立,
则x2-tx+t≥0对任意的正数恒成立,
则t>0且
| 4t-t2 |
| 4 |
解得:t∈(0,4],
故选:C.
点评:本题考查的知识点是对数函数的图象和性质,二次函数的图象和性质,恒成立问题,难度中档.

练习册系列答案
相关题目
点P为△ABC所在平面内一点,若
•(
-
)=0,则直线CP一定经过△ABC的( )
| CP |
| CA |
| CB |
| A、内心 | B、垂心 | C、外心 | D、重心 |
已知复数z=a+bi(a∈R,b∈R)且a+b=1,则下列结论错误的是( )
| A、z可能为实数 | ||||
| B、z不可能为纯虚数 | ||||
C、若z的共轭复数为z,则z•
| ||||
D、|z|的最小值为
|
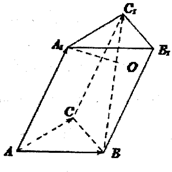 如图所示,三棱柱ABC-A1B1C1中,AA1=2AB=2AC=2.∠A1AB=∠A1AC=∠BAC=60°,设
如图所示,三棱柱ABC-A1B1C1中,AA1=2AB=2AC=2.∠A1AB=∠A1AC=∠BAC=60°,设