题目内容
5.已知数列{an}的前n项和Sn=$\frac{3}{2}$(3n-1),则数列{$\frac{1}{(lo{g}_{3}{a}_{n+1})(lo{g}_{3}{a}_{n+2})}$}的前10项和为( )| A. | $\frac{5}{6}$ | B. | $\frac{11}{12}$ | C. | $\frac{10}{11}$ | D. | $\frac{5}{12}$ |
分析 利用递推关系可得an,再利用“裂项求和”即可得出.
解答 解:∵数列{an}的前n项和Sn=$\frac{3}{2}$(3n-1),
∴当n=1时,a1=3;
当n≥2时,an=Sn-Sn-1=$\frac{3}{2}({3}^{n}-1)$-$\frac{3}{2}({3}^{n-1}-1)$,化为:an=3n,
当n=1时,上式成立,
∴an=3n.
则$\frac{1}{(lo{g}_{3}{a}_{n+1})(lo{g}_{3}{a}_{n+2})}$=$\frac{1}{(n+1)(n+2)}$=$\frac{1}{n+1}-\frac{1}{n+2}$.
∴数列{$\frac{1}{(lo{g}_{3}{a}_{n+1})(lo{g}_{3}{a}_{n+2})}$}的前10项和S10=$(\frac{1}{2}-\frac{1}{3})$+$(\frac{1}{3}-\frac{1}{4})$+…+$(\frac{1}{11}-\frac{1}{12})$=$\frac{1}{2}-\frac{1}{12}$=$\frac{5}{12}$.
故选:D.
点评 本题考查了递推关系、“裂项求和”方法,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
13.在正四棱锥P-ABCD中,PA=2,E为PC的中点,若异面直线PA与BE所成角为45°,则四棱锥P-ABCD的高为( )
| A. | $\frac{\sqrt{3}}{3}$ | B. | $\frac{2\sqrt{3}}{3}$ | C. | $\sqrt{3}$ | D. | 2$\sqrt{3}$ |
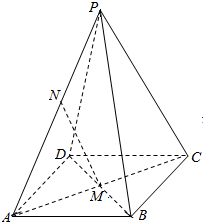 (理科做)如图,正四棱锥P-ABCD中,PA=BD,点M为AC,BD的交点,点N为AP中点.
(理科做)如图,正四棱锥P-ABCD中,PA=BD,点M为AC,BD的交点,点N为AP中点.