题目内容
设函数f(x)=x2+(a+1)x+a,若函数f(x)在区间(1,3)内有零点,则实数a的取值范围为 .
考点:函数零点的判定定理,函数的零点
专题:函数的性质及应用
分析:由f(x)=0得a=-x,即可得到结论.
解答:
解:由f(x)=x2+(a+1)x+a=0的数x2+x+a(x+1)=0,
∵x∈(1,3),
∴方程等价为x+a=0,
即a=-x,
∵x∈(1,3),
∴-x∈(-3,-1),
即a∈(-3,-1),
故答案为:(-3,-1)
∵x∈(1,3),
∴方程等价为x+a=0,
即a=-x,
∵x∈(1,3),
∴-x∈(-3,-1),
即a∈(-3,-1),
故答案为:(-3,-1)
点评:本题主要考查函数零点的判断,利用参数分离法是解决本题的关键.

练习册系列答案
 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案
相关题目
将函数y=sin(x+
)(x∈R)图象上所有的点向左平行移动
个单位长度,再把图象上各点的横坐标扩大到原来的2倍(纵坐标不变),则所得到的图象的解析式为( )
| π |
| 6 |
| π |
| 6 |
A、y=sin(2x+
| ||||
B、y=sin(
| ||||
C、y=sin
| ||||
D、y=cos
|
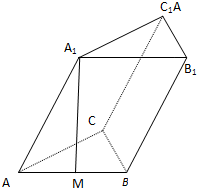 已知斜三棱柱ABC-A1B1C1的底面是正三角形,侧面ABB1A1是菱形,且∠A1AB=60°,M是AB的中点,A1M⊥AC
已知斜三棱柱ABC-A1B1C1的底面是正三角形,侧面ABB1A1是菱形,且∠A1AB=60°,M是AB的中点,A1M⊥AC