题目内容
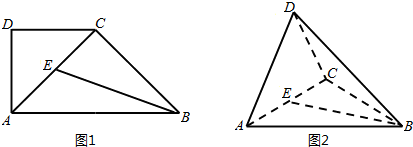
如图1,在直角梯形ABCD中,∠ADC=90°,CD∥AB,AD=CD=
AB=2,点E为AC中点.将△ADC沿AC折起,使平面ADC⊥平面ABC,得到几何体D-ABC,如图2所示.
(1)在CD上找一点F,使AD∥平面EFB;
(2)求点C到平面ABD的距离.
| 1 |
| 2 |
(1)在CD上找一点F,使AD∥平面EFB;
(2)求点C到平面ABD的距离.

考点:点、线、面间的距离计算,直线与平面平行的判定
专题:空间位置关系与距离
分析:(1)取CD的中点F,连结EF,BF,在△ACD中,可证AD∥EF,又EF⊆平面EFB AD?平面EFB,可证AD∥平面EFB.
(2)设点C到平面ABD的距离为h,由于可证AD⊥BD,可得S△ADB=2
,又三棱锥B-ACD的高BC=2
,S△ACD=2,由
×2
h=
×2×2
即可解得点C到平面ABD的距离.
(2)设点C到平面ABD的距离为h,由于可证AD⊥BD,可得S△ADB=2
| 3 |
| 2 |
| 1 |
| 3 |
| 2 |
| 1 |
| 3 |
| 2 |
解答:
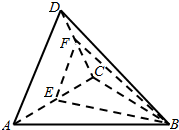 (1)取CD的中点F,连结EF,BF,
(1)取CD的中点F,连结EF,BF,
在△ACD中,∵E,F分别为AC,DC的中点,
∴EF为△ACD的中位线
∴AD∥EF,
EF⊆平面EFB,AD?平面EFB
∴AD∥平面EFB.
(2)设点C到平面ABD的距离为h,
∵平面ADC⊥平面ABC,且BC⊥AC,
∴BC⊥平面ADC,
∴BC⊥AD,而AD⊥DC•
∴AD⊥平面BCD,即AD⊥BD•
∴S△ADB=2
•
∴三棱锥B-ACD的高BC=2
,S△ACD=2,
∴
×2
h=
×2×2
∴可解得:h=2.
 (1)取CD的中点F,连结EF,BF,
(1)取CD的中点F,连结EF,BF,在△ACD中,∵E,F分别为AC,DC的中点,
∴EF为△ACD的中位线
∴AD∥EF,
EF⊆平面EFB,AD?平面EFB
∴AD∥平面EFB.
(2)设点C到平面ABD的距离为h,
∵平面ADC⊥平面ABC,且BC⊥AC,
∴BC⊥平面ADC,
∴BC⊥AD,而AD⊥DC•
∴AD⊥平面BCD,即AD⊥BD•
∴S△ADB=2
| 3 |
∴三棱锥B-ACD的高BC=2
| 2 |
∴
| 1 |
| 3 |
| 2 |
| 1 |
| 3 |
| 2 |
∴可解得:h=2.
点评:本题主要考查了直线与平面平行的判定,考查了点、线、面间的距离计算,考查了空间想象能力和转化思想,属于中档题.

练习册系列答案
相关题目
已知高为1的梯形ABCD内接于半径为1的圆O,若梯形的上底CD=1,则(
+
)•
=( )
| OA |
| OB |
| OC |
| A、0 | ||||
B、
| ||||
C、
| ||||
D、
|
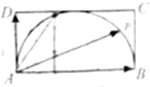 如图,矩形ABCD中,AB=2AD=2,点P在以AB为直径的半圆上移动,若
如图,矩形ABCD中,AB=2AD=2,点P在以AB为直径的半圆上移动,若| AP |
| AB |
| AD |
A、
| ||||
B、
| ||||
| C、2 | ||||
D、
|
若曲线y=x2+ax+b在点(1,1)处的切线为3x-y-2=0,则有( )
| A、a=-1,b=1 |
| B、a=-1,b=-1 |
| C、a=-2,b=1 |
| D、a=2,b=-1 |
下列式子中成立的是(假定各式均有意义)( )
| A、logax•logay=loga(x+y) | |||||
| B、(logax)n=nlogax | |||||
C、
| |||||
D、
|
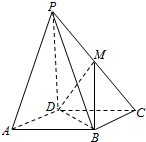 在四棱锥P-ABCD中,PD⊥平面ABCD,底面ABCD是边长为2的正方形,且PD=AB.
在四棱锥P-ABCD中,PD⊥平面ABCD,底面ABCD是边长为2的正方形,且PD=AB. 如图是某几何体的三视图,试求它的体积(单位:cm).
如图是某几何体的三视图,试求它的体积(单位:cm).