题目内容
已知函数f1(x)=|x-1|,f2(x)=
x+1,g(x)=
+
,若a,b∈[-1,5],且当x1,x2∈[a,b]时,
>0恒成立,则b-a的最大值为( )
| 1 |
| 3 |
| f1(x)+f2(x) |
| 2 |
| |f1(x)-f2(x)| |
| 2 |
| g(x1)-g(x2) |
| x1-x2 |
| A、2 | B、3 | C、4 | D、5 |
考点:函数恒成立问题
专题:函数的性质及应用
分析:由f1(x)=|x-1|,f2(x)=
x+1,g(x)=
+
分段求出g(x),分析其单调性,由x1,x2∈[a,b]时,
>0恒成立说明函数在[a,b]上为增函数,求出a为0,b等于5,则b-a的最大值可求.
| 1 |
| 3 |
| f1(x)+f2(x) |
| 2 |
| |f1(x)-f2(x)| |
| 2 |
| g(x1)-g(x2) |
| x1-x2 |
解答:
解:∵a,b∈[-1,5],且x1,x2∈[a,b],
∴a<b,
∵
>0恒成立,
∴g(x)在区间[a,b]上单调第增,
∵函数f1(x)=|x-1|,f2(x)=
x+1,g(x)=
+
,
∴g(x)=
当x∈[-1,0)时,g(x)=1-x,单调减;
当x∈[0,3]时,g(x)=
x+1,单调增;
当x∈[3,5]时,g(x)=x-1,单调递增.
∴a=0,b=5.
b-a的最大值为5-0=5.
故选:D.
∴a<b,
∵
| g(x1)-g(x2) |
| x1-x2 |
∴g(x)在区间[a,b]上单调第增,
∵函数f1(x)=|x-1|,f2(x)=
| 1 |
| 3 |
| f1(x)+f2(x) |
| 2 |
| |f1(x)-f2(x)| |
| 2 |
∴g(x)=
|
当x∈[-1,0)时,g(x)=1-x,单调减;
当x∈[0,3]时,g(x)=
| 1 |
| 3 |
当x∈[3,5]时,g(x)=x-1,单调递增.
∴a=0,b=5.
b-a的最大值为5-0=5.
故选:D.
点评:本题考查了恒成立问题,考查了数学转化思想方法,解得的关键是对题意的理解,是中档题.

练习册系列答案
相关题目
如图,若N=5时,则输出的数等于( )


A、
| ||
B、
| ||
C、
| ||
D、
|
A、B是双曲线
-
=1右支上的两点,若弦AB的中点到Y轴的距离是4,则|AB|的最大值为( )
| x2 |
| 4 |
| y2 |
| 5 |
| A、2 | B、4 | C、6 | D、8 |
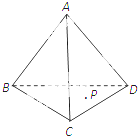 如图,在四面体A-BCD中,△BCD是正三角形,侧棱AB、AC、AD两两垂直且相等,设P为四面体A-BCD表面(含棱)上的一点,由点P到四个顶点的距离组成的集合记为M,如果集合M中有且只有2个元素,那么符合条件的点P有( )
如图,在四面体A-BCD中,△BCD是正三角形,侧棱AB、AC、AD两两垂直且相等,设P为四面体A-BCD表面(含棱)上的一点,由点P到四个顶点的距离组成的集合记为M,如果集合M中有且只有2个元素,那么符合条件的点P有( )| A、4个 | B、6个 | C、8个 | D、14个 |
执行如图所示的程序框图,则输出的a=( )


A、
| ||
B、-
| ||
| C、5 | ||
D、
|
在抛物线y2=4x上恒有两点关于直线l:y=kx+3则对称,k的取值范围是( )
| A、-1<k<0 |
| B、0<k<1 |
| C、-1≤k≤0 |
| D、0≤k≤1 |
已知“渐升数”是指每一位数字比其左边的数字大的正整数(如236),那么任取一个三位数,它是渐升数的概率为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
直线x+
y-m=0与圆x2+y2=1在第一象限内有两个不同的交点,则m的取值范围是( )
| 3 |
| A、(1,2) | ||
B、(
| ||
C、(1,
| ||
D、(
|