题目内容
10.已知$f(x)={sin^2}x+cosx,x∈[{-\frac{π}{3},\frac{2π}{3}}]$,则f(x)的值域为[$\frac{1}{4}$,$\frac{5}{4}$].分析 化简函数f(x),利用二次函数与三角函数的图象和性质,求出函数f(x)的值域即可.
解答 解:∵f(x)=sin2x+cosx=1-cos2x+cosx=-${(cosx-\frac{1}{2})}^{2}$+$\frac{5}{4}$,
且x∈[-$\frac{π}{3}$,$\frac{2π}{3}$],
∴cosx∈[-$\frac{1}{2}$,$\frac{1}{2}$],
∴-1≤cosx-$\frac{1}{2}$≤0,
∴-1≤-${(cosx-\frac{1}{2})}^{2}$≤0,
∴$\frac{1}{4}$≤-${(cosx-\frac{1}{2})}^{2}$≤$\frac{5}{4}$,
即函数f(x)的值域为[$\frac{1}{4}$,$\frac{5}{4}$].
故答案为:[$\frac{1}{4}$,$\frac{5}{4}$].
点评 本题考查了三角函数的化简与求值的应用问题,也考查了求函数最值的应用问题,是基础题目.

练习册系列答案
 期末复习检测系列答案
期末复习检测系列答案 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案
相关题目
18.已知sin(θ+$\frac{π}{2}$)<0,cos(θ-$\frac{π}{2}$)>0,则下列不等式关系必定成立的是( )
| A. | tan2$\frac{θ}{2}$<1 | B. | tan2$\frac{θ}{2}$>1 | C. | sin$\frac{θ}{2}$>cos$\frac{θ}{2}$ | D. | sin$\frac{θ}{2}$<cos$\frac{θ}{2}$ |
18.三棱锥P-ABC中,PA⊥底面ABC,PA=3,底面ABC是边长为2的正三角形,则三棱锥P-ABC的体积等于( )
| A. | 3$\sqrt{3}$ | B. | $\sqrt{3}$ | C. | 2$\sqrt{3}$ | D. | 4$\sqrt{3}$ |
5.下面各组函数中为相同函数的是( )
| A. | f(x)=$\sqrt{(x-1)^{2}}$,g(x)=x-1 | B. | f(x)=$\sqrt{{x}^{2}-1}$,g(x)=$\sqrt{x+1}$•$\sqrt{x-1}$ | ||
| C. | f(x)=ln ex与g(x)=elnx | D. | f(x)=(x-1)0与g(x)=$\frac{1}{(x-1)^{0}}$ |
15.圆x2+y2=4与圆x2+y2-4y+3=0的位置关系是( )
| A. | 相离 | B. | 相交 | C. | 外切 | D. | 内切 |
19.已知集合A={x|x2<1},集合B={x|$\frac{1}{x}$<1},则A∩B=( )
| A. | (-1,0) | B. | (0,1) | C. | (1,+∞) | D. | ∅ |
20.函数f(x)=x2-ln|x|的大致图象为( )
| A. | 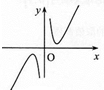 | B. | 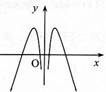 | C. | 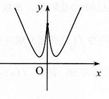 | D. | 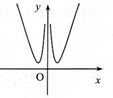 |