题目内容
1．如果直线L1：y=2x+1与椭圆$\frac{x^2}{9}+\frac{y^2}{4}=1$相交于A、B两点，直线L2与该椭圆相交于C、D两点，且ABCD是平行四边形，则L2的方程是y=2x-1．分析 由ABCD是平行四边形可知直线l1∥l2，再由l1过点（0，1），知l2过点（0，-1），由此可导出l2的方程．
解答 
解：由题意可知，直线l1∥l2，
∴l2的斜率k=2．
∵ABCD是平行四边形，l1过点（0，1），
∴l2过点（0，-1），
∴直线l2的方程是y+1=2x，即y=2x-1．
故答案为：y=2x-1；
点评 本题考查椭圆和直线的性质，作出草图，数形结合效果好．
练习册系列答案
相关题目
9．已知向量$\overrightarrow{a}$，$\overrightarrow{b}$，则下列关系正确的是（ ）
| A． | |$\overrightarrow{a}•\overrightarrow{b}$|=|$\overrightarrow{a}$||$\overrightarrow{b}$| | B． | |$\overrightarrow{a}•\overrightarrow{b}$|≤|$\overrightarrow{a}$||$\overrightarrow{b}$| | ||
| C． | |$\overrightarrow{a}•\overrightarrow{b}$|≥|$\overrightarrow{a}$||$\overrightarrow{b}$| | D． | 以上答案都不正确 |
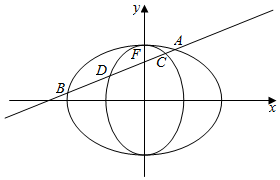如图的椭圆C1，C2的离心率相等，中心均为坐标原点，焦点分别在x轴和y轴上，且两椭圆都过点（0，$\sqrt{2}$），设点F是椭圆C2的上焦点，过点F的动直线l交椭圆C1于A，B两点，交椭圆C2于C，D两点，当直线l经过椭圆C1的左焦点时，$\frac{|AB|}{|CD|}$=$\frac{5\sqrt{2}}{4}$．