题目内容
已知数列{an}的前n项和为Sn,a1=1,且Sn-1+
+2=0(n≥2).
(1)写出S1,S2,S3,S4.(不用写求解过程)
(2)猜想Sn的表达式,并用数学归纳法证明.
| 1 |
| Sn |
(1)写出S1,S2,S3,S4.(不用写求解过程)
(2)猜想Sn的表达式,并用数学归纳法证明.
考点:数学归纳法,数列的求和
专题:点列、递归数列与数学归纳法
分析:第(1)问,因为a1=s1,代入Sn-1+
+2=0(n≥2)可得S2,依此类推,可得S3,S4;
第(2)问,根据第一问结果,猜想出Sn的表达式,然后用数学归纳法证明,先验证n=1时结论成立,然后写出假设,即n=k时,结论成立,利用Sn-1+
+2=0(n≥2),将假设代入上式,解出Sk+1,从而证明n=k+1时结论成立.
| 1 |
| Sn |
第(2)问,根据第一问结果,猜想出Sn的表达式,然后用数学归纳法证明,先验证n=1时结论成立,然后写出假设,即n=k时,结论成立,利用Sn-1+
| 1 |
| Sn |
解答:
解:由已知得(1)S1=1, S2=-
, S3=-
, S4=-
(2)猜想Sn=
,
下面用数学归纳法证明:①当n=1时,S1=-
=1,猜想成立;
②假设当n=k(k∈N★)猜想成立,即Sk=-
,
那么∵Sk+
+2=0,
∴
=-2-Sk=-2+
=-
∴Sk+1=-
=
,所以当n=k+1时猜想成立
由①和②,可知猜想对任何n∈N★都成立.
| 1 |
| 3 |
| 3 |
| 5 |
| 5 |
| 7 |
(2)猜想Sn=
| 2n-3 |
| 2n-1 |
下面用数学归纳法证明:①当n=1时,S1=-
| 2×1-3 |
| 2×1-1 |
②假设当n=k(k∈N★)猜想成立,即Sk=-
| 2k-3 |
| 2k-1 |
那么∵Sk+
| 1 |
| Sk+1 |
∴
| 1 |
| Sk+1 |
| 2k-3 |
| 2k-1 |
| 2k+1 |
| 2k-1 |
∴Sk+1=-
| 2k-1 |
| 2k+1 |
| 2(k+1)-3 |
| 2(k+1)-1 |
由①和②,可知猜想对任何n∈N★都成立.
点评:利用数学归纳法证明与自然数有关的数学命题,关键在于第二步证明n=k+1时命题成立,一般是找到n=k时与n=k+1时的要证的结论之间的关系,然后将假设代入这个关系式,求出(或者变形得到)我们要的n=k+1时的结论;再就是注意证明时的模式,即(1)验证n取初始值时命题成立,(2)写出假设,由此结合已知推出n=k+1时的结论成立;(3)综上,下结论.

练习册系列答案
相关题目
函数f(x)=x2-x的零点个数是( )
| A、3 | B、2 | C、1 | D、0 |
函数f(x)=lg
的图象( )
| 1+sinx |
| cosx |
| A、关于x轴对称 |
| B、关于y轴对称 |
| C、关于原点对称 |
| D、关于直线y=x对称 |
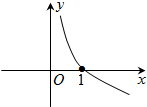 已知函数f(x)的导函数图象如图所示,若△ABC是以角C为钝角的钝角三角形,则一定成立的是( )
已知函数f(x)的导函数图象如图所示,若△ABC是以角C为钝角的钝角三角形,则一定成立的是( )| A、f(sinA)>f(cosB) |
| B、f(sinA)<f(cosB) |
| C、f(sinA)>f(sinB) |
| D、f(cosA)<f(cosB) |
 在平面直角坐标系xOy中,椭圆E:
在平面直角坐标系xOy中,椭圆E: 2013年某市某区高考文科数学成绩抽样统计如下表:
2013年某市某区高考文科数学成绩抽样统计如下表: