题目内容
14.在平面直角坐标系xOy中,曲线y=x2-6x+1与坐标轴的交点都在圆C上.(1)求圆C的方程;
(2)求圆被直线x-y-1=0所截得的弦长.
分析 (1)求出曲线y=x2-6x+1与坐标轴的交点,进而确定圆心与半径,即可求圆C的方程;
(2)求出圆心到直线的距离,利用勾股定理求圆被直线x-y-1=0所截得的弦长.
解答 解:(1)曲线y=x2-6x+1与y轴的交点为(0,1),
与x轴的交点为(3±2$\sqrt{2}$,0),
故可设C的圆心为(3,t),则有9+(t-1)2=8+t2,解得t=1,
则圆C的半径为$\sqrt{9}$=3,
所以圆C的方程为(x-3)2+(y-1)2=9;
(2)圆心到直线的距离d=$\frac{|3-1-1|}{\sqrt{2}}$=$\frac{1}{\sqrt{2}}$,
所以圆被直线x-y-1=0所截得的弦长为2$\sqrt{9-\frac{1}{2}}$=$\sqrt{34}$.
点评 本题考查圆的方程,考查直线与圆的位置关系,考查学生的计算能力,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
3.已知P(8,a)在抛物线y2=4px上,且P到焦点的距离为10,则焦点到准线的距离为( )
| A. | 2 | B. | 4 | C. | 8 | D. | 16 |
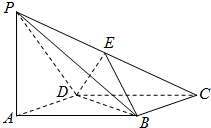 如图,四棱锥P-ABCD中,侧棱PA⊥底面ABCD,底面ABCD为菱形,E为侧棱PC上一点.
如图,四棱锥P-ABCD中,侧棱PA⊥底面ABCD,底面ABCD为菱形,E为侧棱PC上一点. 如图,在正方体ABCD-A1B1C1D1中,点E,F分别是上底面A1B1C1D1和侧面CDD1C1的中心.
如图,在正方体ABCD-A1B1C1D1中,点E,F分别是上底面A1B1C1D1和侧面CDD1C1的中心.