题目内容

20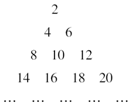．把正偶数数列{2n}的各项从小到大依次排成如图的三角形数阵，记M（r，t）表示该数阵中第r行的第t个数，则数阵中的数2 018对应于（45，19）．

分析 由图可得数阵中的前n行共有1+2+3+…+n=$\frac{n（n+1）}{2}$项，进而可得偶数2012对应的位置．

解答 解：由数阵的排列规律知，数阵中的前n行共有1+2+3+…+n=$\frac{n（n+1）}{2}$项，
当n=44时，共有990项，又数阵中的偶数2018是数列{an }的第1009项，
且$\frac{44×45}{2}$+19=1009，因此2018是数阵中第45行的第19个数，
故答案为：（45，19）．

点评 本题考查等差数列的通项公式和求和公式，属基础题．

练习册系列答案
相关题目
10．用数学归纳法证明不等式1+$\frac{1}{2}$+$\frac{1}{4}$+…+$\frac{1}{{2}^{n-1}}$＞$\frac{127}{64}$成立，起始值应取为n=8．
11．在三棱柱ABC-A1B1C1中，底面为正三角形，侧棱垂直底面，AB=2，AA1=6．若E，F分别是棱BB1，CC1上的点，且BE=B1E，C1F=$\frac{1}{3}$CC1，则异面直线A1E与AF所成角的余弦值为（　　）
A．-$\frac{\sqrt{65}}{13}$B．$\frac{\sqrt{65}}{13}$C．-$\frac{\sqrt{2}}{10}$D．$\frac{\sqrt{2}}{10}$
8．函数 f （ x）=$\frac{x}{lnx}$（ x＞1）单调递减区间是（　　）
A．（1，+∞）B．（1，e2）C．（e，+∞）D．（1，e）
15．已知函数g（ x）=e x+$\frac{a}{2}$x2，其中a∈R，e=2.71828…为自然对数的 底数，f （ x）是 g（ x）的导函数．
（Ⅰ）求 f（ x） 的极值；
（Ⅱ）若a=-1，证明：当 x1≠x2，且f （ x1 ）=f （ x2） 时，x1+x2＜0．
5．已知函数f （ x）=ax3+bx2+cx+d 的图象如图所示，则$\frac{b+1}{a+1}$的取值范围是（　　） 
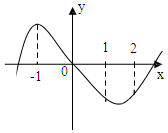
A．（-$\frac{3}{2}$，$\frac{1}{2}$ ）B．（-$\frac{2}{5}$，1）C．（-$\frac{1}{2}$，$\frac{3}{2}$）D．（-$\frac{3}{2}$，1）
12．已知数列{an}是等差数列，a1=cot585°，a6=11a1，设Sn为数列{（-1）nan}的前n项和，则S2017=（　　）
A．3022B．-3022C．2017D．-2017
9．两个变量y与x的回归模型中，分别选择了4个不同模型，它们对应的回归系数r如下，其中变量之间线性相关程度最高的模型是（　　）
A．模型1对应的r为-0.98B．模型2对应的r为0.80
C．模型3对应的r为0.50D．模型4对应的r为-0.25
10．若一个几何体的三视图都是如图所示的边长为2的正方形，则该几何体的外接球的表面积是（　　）
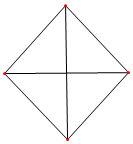
A．πB．2πC．4πD．8π

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网