题目内容
10.用数学归纳法证明不等式1+$\frac{1}{2}$+$\frac{1}{4}$+…+$\frac{1}{{2}^{n-1}}$>$\frac{127}{64}$成立,起始值应取为n=8.分析 利用等比数列求和公式,求出左边的和,再解相应的不等式,求出结果.
解答 解:不等式左边=$\frac{1-\frac{1}{{2}^{n}}}{1-\frac{1}{2}}$=2-21-n,
当n=1,2,3,…6,7时不等式不成立.
当n=8,9…时,不等式成立,
初始值至少应取8.
故答案为:8.
点评 本题主要考查数学归纳法,起始值的验证,考查学生的计算能力,属于基础题.

练习册系列答案
 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目
20.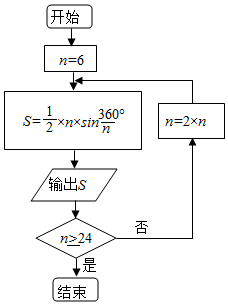 公元263年左右,我国数学家刘徽发现当圆内接正多边形的边数无限增加时,多边形的面积可无限逼近圆的面积,并创立了“割圆术”.利用“割圆术”刘徽得到了圆周率精确到小数点后两位的近似值3.14,这就是著名的“徽率”.如图是利用刘徽的“割圆术”思想设计的一个程序框图,其中n表示圆内接正多边形的边数,执行此算法输出的圆周率的近似值依次为(参考数据:$\sqrt{3}$≈1.732,sin15°≈0.2588,sin75°≈0.1305)( )
公元263年左右,我国数学家刘徽发现当圆内接正多边形的边数无限增加时,多边形的面积可无限逼近圆的面积,并创立了“割圆术”.利用“割圆术”刘徽得到了圆周率精确到小数点后两位的近似值3.14,这就是著名的“徽率”.如图是利用刘徽的“割圆术”思想设计的一个程序框图,其中n表示圆内接正多边形的边数,执行此算法输出的圆周率的近似值依次为(参考数据:$\sqrt{3}$≈1.732,sin15°≈0.2588,sin75°≈0.1305)( )
 公元263年左右,我国数学家刘徽发现当圆内接正多边形的边数无限增加时,多边形的面积可无限逼近圆的面积,并创立了“割圆术”.利用“割圆术”刘徽得到了圆周率精确到小数点后两位的近似值3.14,这就是著名的“徽率”.如图是利用刘徽的“割圆术”思想设计的一个程序框图,其中n表示圆内接正多边形的边数,执行此算法输出的圆周率的近似值依次为(参考数据:$\sqrt{3}$≈1.732,sin15°≈0.2588,sin75°≈0.1305)( )
公元263年左右,我国数学家刘徽发现当圆内接正多边形的边数无限增加时,多边形的面积可无限逼近圆的面积,并创立了“割圆术”.利用“割圆术”刘徽得到了圆周率精确到小数点后两位的近似值3.14,这就是著名的“徽率”.如图是利用刘徽的“割圆术”思想设计的一个程序框图,其中n表示圆内接正多边形的边数,执行此算法输出的圆周率的近似值依次为(参考数据:$\sqrt{3}$≈1.732,sin15°≈0.2588,sin75°≈0.1305)( )| A. | 2.598,3,3.1048 | B. | 2.598,3,3.1056 | C. | 2.578,3,3.1069 | D. | 2.588,3,3.1108 |
1.下列语句不是命题的是( )
| A. | -3>4 | B. | 0.3是整数 | C. | a>3 | D. | 4是3的约数 |
18.下列求导结果正确的是( )
| A. | (a-x2)′=1-2x | B. | (2$\sqrt{{x}^{3}}$)′=3$\sqrt{x}$ | C. | (cos60°)′=-sin60° | D. | [ln(2x)]′=$\frac{1}{2x}$ |
15.我们知道,在长方形ABCD中,如果设AB=a,BC=b,那么长方形ABCD的外接圆的半径R满足4R2=a2+b2,类比上述结论,在长方体ABCD-A1B1C1D1中,如果设AB=a,AD=b,AA1=c,那么长方体ABCD-A1B1C1D1的外接球的半径R满足的关系式是( )
| A. | 4R2=a3+b3+c3 | B. | 8R2=a2+b2+c2 | C. | 8R3=a3+b3+c3 | D. | 4R2=a2+b2+c2 |
2.已知$\vec a=(2,t,t),\vec b=(1-t,2t-1,0)$,则$|\vec b-\vec a|$的最小值是( )
| A. | $\sqrt{2}$ | B. | $\sqrt{3}$ | C. | $\sqrt{5}$ | D. | $\sqrt{6}$ |
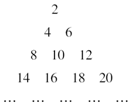 把正偶数数列{2n}的各项从小到大依次排成如图的三角形数阵,记M(r,t)表示该数阵中第r行的第t个数,则数阵中的数2 018对应于(45,19).
把正偶数数列{2n}的各项从小到大依次排成如图的三角形数阵,记M(r,t)表示该数阵中第r行的第t个数,则数阵中的数2 018对应于(45,19).