题目内容
数列{an}中相邻两项an与an+1是方程x2+3nx+bn=0的两根,已知a10=-13,则b21等于 .
考点:数列递推式
专题:等差数列与等比数列
分析:由于an与an+1是方程x2+3nx+bn=0的两根,可得an+an+1=-3n,an•an+1=bn.由an+an+1=-3n,an+1+an+2=-3(n+1),可得an+2-an=-3,可得n为奇数、偶数时分别成等差数列,由a10=-13,可得a22,进而得到a21.
解答:
解:∵an与an+1是方程x2+3nx+bn=0的两根,
∴an+an+1=-3n,an•an+1=bn.
由an+an+1=-3n,an+1+an+2=-3(n+1),
∴an+2-an=-3,
可得n为奇数、偶数时分别成等差数列,
由a10=-13,
∴a22=-13+6×(-3)=-31,
∴a21=-3×21-(-31)=-32,
∴b21=a21•a22=-31×(-32)=992.
故答案为:992.
∴an+an+1=-3n,an•an+1=bn.
由an+an+1=-3n,an+1+an+2=-3(n+1),
∴an+2-an=-3,
可得n为奇数、偶数时分别成等差数列,
由a10=-13,
∴a22=-13+6×(-3)=-31,
∴a21=-3×21-(-31)=-32,
∴b21=a21•a22=-31×(-32)=992.
故答案为:992.
点评:本题考查了等差数列的通项公式、一元二次方程的根与系数的关系、递推式的应用,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
已知x=a1是函数f(x)=
x4+bx2+cx+d的唯一极值点且为最小值点,若存在a2∈(a1,a1+1)使得f′(a2)=0,则关于x的函数g(x)=f(x)-
x2+a1x在(a1,a2)上的零点的说法正确的是( )
| 1 |
| 4 |
| 1 |
| 2 |
| A、至多只有一个零点 |
| B、只有唯一的零点 |
| C、可能存在两个零点 |
| D、可能存在四个零点 |
已知平面向量
与
的夹角为
,且|
|=1,|
+2
|=2
,则|
|=( )
| a |
| b |
| π |
| 3 |
| b |
| a |
| b |
| 3 |
| a |
| A、1 | ||
B、
| ||
| C、3 | ||
| D、2 |
实数x,y满足
,则z=3x-y的最小值是( )
|
| A、-4 | B、-2 | C、0 | D、4 |
执行如图中的程序框图,若p=0.8,则输出的n=( )
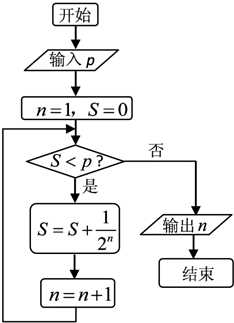

| A、2 | B、3 | C、5 | D、4 |
 一个几何体的三视图如图所示,其中主视图、俯视图与左视图均是半径为2的圆,则这个几何体的表面积是
一个几何体的三视图如图所示,其中主视图、俯视图与左视图均是半径为2的圆,则这个几何体的表面积是


