题目内容
10. 如图,在三棱柱ABC-A1B1C1中,CC1⊥底面ABC,AC⊥CB,点M和N分别是B1C1和BC的中点.
如图,在三棱柱ABC-A1B1C1中,CC1⊥底面ABC,AC⊥CB,点M和N分别是B1C1和BC的中点.(1)求证:MB∥平面AC1N;
(2)求证:AC⊥MB.
分析 (1)证明MC1NB为平行四边形,所以C1N∥MB,即可证明MB∥平面AC1N;
(2)证明AC⊥平面BCC1B1,即可证明AC⊥MB.
解答 证明:(1)证明:在三棱柱ABC-A1B1C1中,因为点M,N分别是B1C1,BC的中点,
所以C1M∥BN,C1M=BN.
所以MC1NB为平行四边形.
所以C1N∥MB.
因为C1N?平面AC1N,MB?平面AC1N,
所以MB∥平面AC1N;
(2)因为CC1⊥底面ABC,
所以AC⊥CC1.
因为AC⊥BC,BC∩CC1=C,
所以AC⊥平面BCC1B1.
因为MB?平面BCC1B1,
所以AC⊥MB.
点评 本题考查线面平行的判定,考查线面垂直的判定与性质,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
 期末100分闯关海淀考王系列答案
期末100分闯关海淀考王系列答案 小学能力测试卷系列答案
小学能力测试卷系列答案
相关题目
5.如果圆C:(x-a)2+(y-3)2=5的一条切线的方程为y=2x,那么a的值为( )
| A. | 4或1 | B. | -1或4 | C. | 1或-4 | D. | -1或-4 |
2.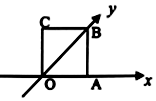 如图水平放置的一个平面图形的直观图是边长为1cm的正方形,则原图形的周长是( )
如图水平放置的一个平面图形的直观图是边长为1cm的正方形,则原图形的周长是( )
 如图水平放置的一个平面图形的直观图是边长为1cm的正方形,则原图形的周长是( )
如图水平放置的一个平面图形的直观图是边长为1cm的正方形,则原图形的周长是( )| A. | 8cm | B. | 6cm | C. | $2(1+\sqrt{3})cm$ | D. | $2(1+\sqrt{2})cm$ |
19.若复数z满足(1+i)z=i(i是虚数单位),则z的虚部为( )
| A. | $\frac{1}{2}$ | B. | -$\frac{1}{2}$ | C. | $\frac{1}{2}$i | D. | -$\frac{1}{2}i$ |
20.一架战斗机以1000$\sqrt{2}$千米/小时速度朝东偏北45°方向水平飞行,发现正东100千米外同高度有一架民航飞机正在以800千米/小时速度朝正北飞行,如双方都不改变速度与航向,两机最小距离在哪个区间内(单位:千米)( )
| A. | (0,5) | B. | (5,10) | C. | (10,15) | D. | (15,20) |