题目内容
11.已知曲线C的参数方程是$\left\{\begin{array}{l}{x=\sqrt{3}cosα}\\{y=sinα}\end{array}\right.$(α为参数)(1)将C的参数方程化为普通方程;
(2)在直角坐标系xOy中,P(0,2),以原点O为极点,x轴的正半轴为极轴,建立极坐标系,直线l的极坐标方程为ρcosθ+$\sqrt{3}$ρsinθ+2$\sqrt{3}$=0,Q为C上的动点,求线段PQ的中点M到直线l的距离的最小值.
分析 (1)消去参数,将C的参数方程化为普通方程;
(2)将直线l 的方程化为普通方程为x+$\sqrt{3}$y+2$\sqrt{3}$=0.设Q($\sqrt{3}$cosα,sinα),则M($\frac{\sqrt{3}}{2}$cosα,1+$\frac{1}{2}$sinα),利用点到直线的距离公式,即可求线段PQ的中点M到直线l的距离的最小值.
解答 解:(1)消去参数得,曲线C的普通方程得$\frac{{x}^{2}}{3}+{y}^{2}$=1. …(5分)
(2)将直线l 的方程化为普通方程为x+$\sqrt{3}$y+2$\sqrt{3}$=0.
设Q($\sqrt{3}$cosα,sinα),则M($\frac{\sqrt{3}}{2}$cosα,1+$\frac{1}{2}$sinα),
∴d=$\frac{|\frac{\sqrt{3}}{2}cosα+\sqrt{3}+\frac{\sqrt{3}}{2}sinα+2\sqrt{3}|}{2}$=$\frac{|\frac{\sqrt{6}}{2}sin(α+\frac{π}{4})+3\sqrt{3}|}{2}$,
∴最小值是$\frac{6\sqrt{3}-\sqrt{6}}{4}$.…(10分)
点评 本题考查参数方程、普通方程、极坐标方程的转化,考查点到直线的距离公式,考查学生的计算能力,属于中档题.

练习册系列答案
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
2.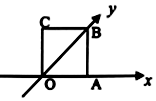 如图水平放置的一个平面图形的直观图是边长为1cm的正方形,则原图形的周长是( )
如图水平放置的一个平面图形的直观图是边长为1cm的正方形,则原图形的周长是( )
 如图水平放置的一个平面图形的直观图是边长为1cm的正方形,则原图形的周长是( )
如图水平放置的一个平面图形的直观图是边长为1cm的正方形,则原图形的周长是( )| A. | 8cm | B. | 6cm | C. | $2(1+\sqrt{3})cm$ | D. | $2(1+\sqrt{2})cm$ |
19.若复数z满足(1+i)z=i(i是虚数单位),则z的虚部为( )
| A. | $\frac{1}{2}$ | B. | -$\frac{1}{2}$ | C. | $\frac{1}{2}$i | D. | -$\frac{1}{2}i$ |
16.“a=0”是“直线l1:ax+y-1=0与直线l2:x+ay-1=0垂直”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
20.一架战斗机以1000$\sqrt{2}$千米/小时速度朝东偏北45°方向水平飞行,发现正东100千米外同高度有一架民航飞机正在以800千米/小时速度朝正北飞行,如双方都不改变速度与航向,两机最小距离在哪个区间内(单位:千米)( )
| A. | (0,5) | B. | (5,10) | C. | (10,15) | D. | (15,20) |
 60名学生某次数学考试成绩(单位:分)的频率分布直方图如图所示,则成绩不低于80分的学生人数是24.
60名学生某次数学考试成绩(单位:分)的频率分布直方图如图所示,则成绩不低于80分的学生人数是24.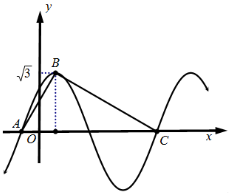 已知函数y=$\sqrt{3}$sin(ωx+$\frac{π}{4}$)(ω>0).
已知函数y=$\sqrt{3}$sin(ωx+$\frac{π}{4}$)(ω>0).