题目内容

9．幂函数y=f（x）经过点（3，$\sqrt{3}$），则f（x）是（　　）
A．偶函数，且在（0，+∞）上是增函数
B．偶函数，且在（0，+∞）上是减函数
C．奇函数，且在（0，+∞）是减函数
D．非奇非偶函数，且在（0，+∞）上是增函数

分析 设出幂函数的解析式，求出自变量的指数，从而求出函数的性质即可．

解答 解：设幂函数的解析式为：y=xα，
将（3，$\sqrt{3}$）代入解析式得：
3α=$\sqrt{3}$，解得α=$\frac{1}{2}$，
∴y=${x}^{\frac{1}{2}}$，
故选：D．

点评 本题考查了求幂函数的解析式，考查函数的奇偶性和单调性问题，是一道基础题．

练习册系列答案
相关题目
4．计算：$\frac{-2\sqrt{3}+i}{1+2\sqrt{3}i}$+（$\frac{\sqrt{2}}{1+i}$）3204+$\frac{（4-8i）^{2}-（-4+8i）^{2}}{\sqrt{11}-\sqrt{7}i}$．
20．设i为虚数单位，则复数$\frac{2+i}{1-2i}$=i．
17．已知函数$f（x）=ax+{log_2}（{2^x}+1）$，其中a∈R．
（1）根据a的不同取值，讨论f（x）的奇偶性，并说明理由；
（2）已知a＞0，函数f（x）的反函数为f-1（x），若函数y=f（x）+f-1（x）在区间[1，2]上的最小值为1+log23，求函数f（x）在区间[1，2]上的最大值．
4．已知函数f=$\left\{\begin{array}{l}{{2}^{x+2}，x＜0}\\{{x}^{3}，x≥0}\end{array}\right.$，则f[f（-1）]=8．
14．如图，O为△ABC的外心，AB=4，AC=2，∠BAC为钝角，M是边BC的中点，则$\overrightarrow{AM}$•$\overrightarrow{AO}$的值为（　　）
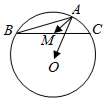
A．4B．5C．7D．6
1．已知各项均不为0的数列{an}的前n项和为Sn，对任意正整数n，有4Sn=（2n+1）an+1．
（1）求a1的值及数列{an}的通项公式；
（2）对一切正整数n，设bn=$\frac{（-1）^{n}4n}{{a}_{n}•{a}_{n+1}}$，求数列{bn}的前n项和Sn．
18．已知在R上可导的函数f（x）的图象如图所示，则不等式f（x）•f′（x）＞0的解集为（-1，2）∪（3，+∞）．
9．如果随机变量ξ～N（μ，σ2），Eξ=3，Dξ=1，P（ξ＜0）=p，则P（ξ＜6）等于（　　）
A．$\frac{1}{2}-p$B．$\frac{1}{2}+p$C．$\frac{1}{2}+\frac{p}{2}$D．1-p

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网