题目内容
14.如图,O为△ABC的外心,AB=4,AC=2,∠BAC为钝角,M是边BC的中点,则$\overrightarrow{AM}$•$\overrightarrow{AO}$的值为( )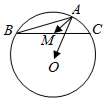
| A. | 4 | B. | 5 | C. | 7 | D. | 6 |
分析 可延长AO交外接圆于点N,并连接BN,CN,从而可得到$∠ABN=\frac{π}{2},∠ACN=\frac{π}{2}$,而由M为BC中点即可得出$\overrightarrow{AM}=\frac{\overrightarrow{AB}+\overrightarrow{AC}}{2}$,从而有$\overrightarrow{AM}•\overrightarrow{AO}=\frac{1}{4}(\overrightarrow{AB}•\overrightarrow{AN}+\overrightarrow{AC}•\overrightarrow{AN})$,显然$\overrightarrow{AB}•\overrightarrow{AN}=|\overrightarrow{AB}{|}^{2},\overrightarrow{AC}•\overrightarrow{AN}=|\overrightarrow{AC}{|}^{2}$,从而便可得出$\overrightarrow{AM}•\overrightarrow{AO}$的值.
解答 解:如图,延长AO交△ABC的外接圆于点N,连接BN,CN;
∵M为边BC中点;
∴$\overrightarrow{AM}=\frac{1}{2}(\overrightarrow{AB}+\overrightarrow{AC})$,且$∠ABN=∠ACN=\frac{π}{2}$;
∴$\overrightarrow{AM}•\overrightarrow{AO}=\frac{1}{4}(\overrightarrow{AB}+\overrightarrow{AC})•\overrightarrow{AN}$
=$\frac{1}{4}(\overrightarrow{AB}•\overrightarrow{AN}+\overrightarrow{AC}•\overrightarrow{AN})$
=$\frac{1}{4}(|\overrightarrow{AB}||\overrightarrow{AN}|cos∠BAN+|\overrightarrow{AC}||\overrightarrow{AN}|cos∠CAN)$
=$\frac{1}{4}(|\overrightarrow{AB}{|}^{2}+|\overrightarrow{AC}{|}^{2})$
=5.
故选B.
点评 考查三角形外接圆的定义,圆的直径对的圆周角为直角,向量加法的平行四边形法则,以及余弦函数的定义,向量数量积的计算公式.

| A. | [2,+∞) | B. | [0,1] | C. | [1,2] | D. | [0,2] |
| A. | 偶函数,且在(0,+∞)上是增函数 | |
| B. | 偶函数,且在(0,+∞)上是减函数 | |
| C. | 奇函数,且在(0,+∞)是减函数 | |
| D. | 非奇非偶函数,且在(0,+∞)上是增函数 |