题目内容

4．若集合M={x|x2-2x＜0}，N={x||x|＞1}，则M∩N=（1，2）．

分析 解x2-2x＜0可得集合M={x|0＜x＜2}，解|x|＞1可得集合N，由交集的定义，分析可得答案．

解答 解：x2-2x＜0?0＜x＜2，则集合M={x|0＜x＜2}=（0，2）
|x|＞1?x＜-1或x＞1，则集合N=（-∞，-1）∪（1，+∞），
则M∩N=（1，2），
故答案为：（1，2）

点评 本题考查集合交集的计算，关键是求出集合集合M、N，注意答案写成集合或区间的形式．

练习册系列答案
相关题目
14．已知集合A={1，2，3}，B={2，3}，则（　　）
A．A∩B=∅B．∁AB=BC．A⊆BD．B$\begin{array}{l}?\\≠\end{array}$A
15．“4＜K＜9”是“方程$\frac{{x}^{2}}{9-k}$+$\frac{{y}^{2}}{k-4}$=1表示的图形为椭圆”的（　　）
A．充分不必要条件B．必要不充分条件
C．充要条件D．既不充分也不必要条件
12．设x∈R，则“x＜-2”是“x2+x≥0”的（　　）
A．充分不必要条件B．必要不充分条件
C．充要条件D．既不充分也不必要条件
19．已知函数f（x）=log2||x|-1|．
（1）作出函数f（x）的大致图象；
（2）指出函数f（x）的奇偶性、单调区间及零点．
9．若an是（2+x）n（n∈N*，n≥2，x∈R）展开式中x2项的二项式系数，则$\lim_{n→∞}（\frac{1}{a_2}+\frac{1}{a_3}+…+\frac{1}{a_n}）$=2．
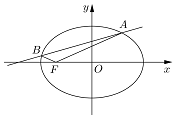16．已知椭圆C以原点为中心，左焦点F的坐标是（-1，0），长轴长是短轴长的$\sqrt{2}$倍，直线l与椭圆C交于点A与B，且A、B都在x轴上方，满足∠OFA+∠OFB=180°；
（1）求椭圆C的标准方程；
（2）对于动直线l，是否存在一个定点，无论∠OFA如何变化，直线l总经过此定点？若存在，求出该定点的坐标；若不存在，请说明理由．
13．已知$\overrightarrow m=（2\sqrt{3}，1）$，$\overrightarrow n=（{cos^2}\frac{A}{2}，sinA）$，A、B、C是△ABC的内角；
（1）当$A=\frac{π}{2}$时，求$|\overrightarrow n|$的值；
（2）若$C=\frac{2π}{3}$，|AB|=3，当$\overrightarrow{m•}\overrightarrow n$取最大值时，求A的大小及边BC的长．
3．已知向量$\overrightarrow{OA}$=（k，12），$\overrightarrow{OB}$=（4，5），$\overrightarrow{OC}$=（10，k），且A、B、C三点共线，当k＜0时，若k为直线的斜率，则过点（2，-1）的直线方程为2x+y-3=0．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网