题目内容
7．函数f（x）=|x2-4|-a恰有两个零点，则实数a的取值范围为a=0或a＞4．分析 画出函数y=|x2-4|，与y=a的图象，利用函数的两个零点，写出结果即可．
解答 
解：函数g（x）=|x2-4|的图象如图所示，
∵函数f（x）=|x2-4|-a恰有两个零点，
∴a=0或a＞4．
故答案为：a=0或a＞4．
点评 本题考查的知识点是根的存在性及根的个数判断，其中熟练掌握函数零点与方程根之间的对应关系是解答的关键．
练习册系列答案
相关题目
17．执行如图所示的程序框图，输出S的值为（ ）
| A． | 45 | B． | 55 | C． | 66 | D． | 110 |
18．已知函数f（x）=|lnx|，若在区间$[\frac{1}{3}，3]$内，曲线g（x）=f（x）-ax与x轴有三个不同的交点，则实数a的取值范围是（ ）
| A． | $[\frac{ln3}{3}，\frac{1}{e}）$ | B． | $[\frac{ln3}{3}，\frac{1}{2e}）$ | C． | $（0，\frac{1}{e}）$ | D． | $（0，\frac{1}{2e}）$ |
15．“4＜K＜9”是“方程$\frac{{x}^{2}}{9-k}$+$\frac{{y}^{2}}{k-4}$=1表示的图形为椭圆”的（ ）
| A． | 充分不必要条件 | B． | 必要不充分条件 | ||
| C． | 充要条件 | D． | 既不充分也不必要条件 |
12．设x∈R，则“x＜-2”是“x2+x≥0”的（ ）
| A． | 充分不必要条件 | B． | 必要不充分条件 | ||
| C． | 充要条件 | D． | 既不充分也不必要条件 |
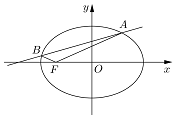已知椭圆C以原点为中心，左焦点F的坐标是（-1，0），长轴长是短轴长的$\sqrt{2}$倍，直线l与椭圆C交于点A与B，且A、B都在x轴上方，满足∠OFA+∠OFB=180°；