题目内容
设函数f(x)=
(2t+1)dt,则数列{f(n)},n∈N*的前n项和的表达式是Sn= .
| ∫ | x 0 |
考点:定积分
专题:计算题,导数的综合应用
分析:根据微积分基本定理以及数列前n项和公式求得即可.
解答:
解:f(x)=
(2t+1)dt=(2t2+t)
=x2+x,
∴f(1)=12+1,f(2)=22+2,…f(n)=n2+n
∴Sn=f(1)+f(2)+…+f(n)
=(12+1)+(22+2)+(32+3)+…+(n2+n)
=(12+22+32+…+n2)+(1+2+3+…+n)
=
+
=
.
故答案为:
| ∫ | x 0 |
| | | x 0 |
∴f(1)=12+1,f(2)=22+2,…f(n)=n2+n
∴Sn=f(1)+f(2)+…+f(n)
=(12+1)+(22+2)+(32+3)+…+(n2+n)
=(12+22+32+…+n2)+(1+2+3+…+n)
=
| n(n+1)(2n+1) |
| 6 |
| n(n+1) |
| 2 |
=
| n(n+1)(n+2) |
| 3 |
故答案为:
| n(n+1)(n+2) |
| 3 |
点评:本题主要考查了微积分基本定理以及数列的求和公式,属于基础题目.

练习册系列答案
 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案
相关题目
如图所示茎叶图记录了甲、乙两组各五名学生在一次英语听力测试中的成绩(单位:分).
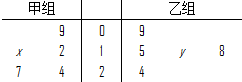
已知甲组数据的平均数为17,乙组数据的中位数为17,则x,y的值分别为( )

已知甲组数据的平均数为17,乙组数据的中位数为17,则x,y的值分别为( )
| A、2,6 | B、2,7 |
| C、3,6 | D、3,7 |