题目内容
某市有大型、中型与小型的商店共1500家，它们的家数之比为3：5：7．为调查商店的每日零售额情况，采用分层抽样的方法抽取一个容量 为90的样本，则样本中大型商店数量为（ ）
| A、12 | B、15 | C、18 | D、24 |
考点：分层抽样方法
专题：概率与统计
分析：根据有大型、中型与小型商店共1500家，它们的家数之比为3：5：7．用分层抽样抽取其中的90家进行调查，做出大型商店所占的比例，得到结果．
解答：
解：∵有大型、中型与小型商店共1500家，它们的家数之比为3：5：7．
用分层抽样抽取其中的90家进行调查，
∴中型商店要抽取90×
=18，
故选：C．
用分层抽样抽取其中的90家进行调查，
∴中型商店要抽取90×
| 3 |
| 3+5+7 |
故选：C．
点评：本题考查分层抽样方法，本题解题的关键是理解在抽样过程中每个个体被抽到的概率相等，本题是一个基础题．
练习册系列答案
阅读快车系列答案
相关题目
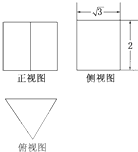如图为一个几何体的三视图，正视图和侧视图均为矩形，俯视图为正三角形，尺寸如图，则该几何体的表面积为（ ）A、14
| ||
B、6+
| ||
C、12+2
| ||
D、16+2
|
下列函数是奇函数的是（ ）
| A、y=x3 | ||
| B、y=2x2-3 | ||
C、y=x
| ||
| D、y=x-2，x∈[0，1] |
已知tanα=2，则
的值（ ）
| 2cosα-3sinα |
| 3cosα+4sinα |
A、
| ||
B、-
| ||
C、
| ||
| D、1 |
函数f(x)=sin2(x+
)-
是（ ）
| π |
| 4 |
| 1 |
| 2 |
| A、最小正周期为π的奇函数 |
| B、最小正周期为π的偶函数 |
| C、最小正周期为2π的奇函数 |
| D、最小正周期为2π的偶函数 |
复数（1+i）2-
（i为虚数单位）的值为 （ ）
| 1-i |
| 1+i |
| A、0 | B、2i | C、3i | D、-4i |