题目内容
下列函数是奇函数的是( )
| A、y=x3 | ||
| B、y=2x2-3 | ||
C、y=x
| ||
| D、y=x-2,x∈[0,1] |
考点:函数奇偶性的判断
专题:函数的性质及应用
分析:要探讨函数的奇偶性,先求函数的定义域,判断其是否关于原点对称,然后探讨f(-x)与f(x)的关系,即可得 函数的奇偶性.
解答:
解:A:y=x3定义域为R,是奇函数.
B:y=2x2-3定义域为R,是偶函数;
C:y=x
定义域为[0,+∞),是非奇非偶函数;
D:y=x-2x∈[0,1],是非奇非偶函数;
故选A.
B:y=2x2-3定义域为R,是偶函数;
C:y=x
| 1 |
| 2 |
D:y=x-2x∈[0,1],是非奇非偶函数;
故选A.
点评:本题考查了函数的奇偶性的判断---定义法,注意定义域,奇偶性的判断,是基础题.

练习册系列答案
 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案
相关题目
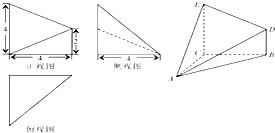 已知某几何体的三视图如图所示,其中俯视图和侧视图都是腰长为4的等腰直角三角形,正视图为直角梯形,则此几何体的体积V为( )
已知某几何体的三视图如图所示,其中俯视图和侧视图都是腰长为4的等腰直角三角形,正视图为直角梯形,则此几何体的体积V为( )| A、32 | ||
| B、16 | ||
C、
| ||
| D、40 |
某市有大型、中型与小型的商店共1500家,它们的家数之比为3:5:7.为调查商店的每日零售额情况,采用分层抽样的方法抽取一个容量 为90的样本,则样本中大型商店数量为( )
| A、12 | B、15 | C、18 | D、24 |
已知在等差数列{an}中,若a1=4,a5=-4,则该数列的公差d等于( )
| A、1 | ||
B、
| ||
| C、-2 | ||
| D、3 |
 100辆汽车在一个时段经过某一雷达测速区,这些汽车运行时速的频率分布直方图如图所示,则这些汽车的平均速度约为
100辆汽车在一个时段经过某一雷达测速区,这些汽车运行时速的频率分布直方图如图所示,则这些汽车的平均速度约为