题目内容
棱锥P-ABCD中,四边形ABCD为平行四边形,AB、AD、AP两两垂直,AB=1,AD=2,AP=3,F为PC的中点,E在PD上,且PD=3PE.
(1)用向量
,
,
表示向量
.
(2)求|
|.
(1)用向量
| AB |
| AD |
| AP |
| EF |
(2)求|
| EF |
考点:空间向量的数量积运算
专题:空间向量及应用
分析:(1)以A为坐标原点,以AB为x轴,以AD这y轴,以AP为z轴,建立空间直角坐标系,利用向量法能求出
=
+
-
.
(2)由
=(
,
,-
),能求出|
|.
| EF |
| 1 |
| 2 |
| AB |
| 1 |
| 6 |
| AD |
| 1 |
| 6 |
| AP |
(2)由
| EF |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 2 |
| EF |
解答:
解:(1)∵AB、AD、AP两两垂直,
∴以A为坐标原点,
以AB为x轴,以AD这y轴,以AP为z轴,
建立空间直角坐标系,
∵AB=1,AD=2,AP=3,
F为PC的中点,E在PD上,且PD=3PE,
∴A(0,0,0),B(1,0,0),C(1,2,0),
P(0,0,3),D(0,2,0),E(0,
,2),F(
,1,
),
∴
=(1,0,0),
=(0,2,0),
=(0,0,3),
∴
=(
,
,-
)
=
+
-
.
(2)∵
=(
,
,-
),
∴|
|=
=
.

∴以A为坐标原点,
以AB为x轴,以AD这y轴,以AP为z轴,
建立空间直角坐标系,
∵AB=1,AD=2,AP=3,
F为PC的中点,E在PD上,且PD=3PE,
∴A(0,0,0),B(1,0,0),C(1,2,0),
P(0,0,3),D(0,2,0),E(0,
| 2 |
| 3 |
| 1 |
| 2 |
| 3 |
| 2 |
∴
| AB |
| AD |
| AP |
∴
| EF |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 2 |
=
| 1 |
| 2 |
| AB |
| 1 |
| 6 |
| AD |
| 1 |
| 6 |
| AP |
(2)∵
| EF |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 2 |
∴|
| EF |
|
| ||
| 6 |
点评:本题考查向量的表示和向量的模的求法,是中档题,解题时要认真审题,注意向量法的合理运用.

练习册系列答案
 永乾教育寒假作业快乐假期延边人民出版社系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案
相关题目
函数f(x)为偶函数,且x∈(-∞,0)时,f(x)=x(x-1),则x∈(0,+∞)时,f(x)为( )
| A、x(x+1) |
| B、-x(-x+1) |
| C、x(-x+1) |
| D、x(x-1) |
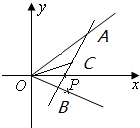 如图所示,射线OA、OB分别与x轴正半轴成45°和30°角,过点P(1,0)作直线AB分别交OA、OB于A、B两点,当AB的中点C恰好落在直线y=
如图所示,射线OA、OB分别与x轴正半轴成45°和30°角,过点P(1,0)作直线AB分别交OA、OB于A、B两点,当AB的中点C恰好落在直线y=